Itō integral
Partial function
| context | $\langle\!\langle \Omega,\mathcal{F},(\mathcal{F}_t)_{t\ge 0},\mathbb{P} \rangle\!\rangle$ … filtered probability space |
| context | $X_t$ … $\mathcal{F}_t$-adapted |
| context | $H_t$ … left-continuous, locally bounded, $\mathcal{F}_t$-adapted |
| let | $h_n=\frac{b-a}n$ |
| let | $\Delta X_{n,i} = X_{a+ih_n}-X_{a+(i-1)h_n}$ |
| definition | todo: type |
| definition | $\int_a^b H_{t-}\,{\mathrm d}X_t := {\mathrm{plim}}_{n \to \infty} \sum_{i=1}^n H_{a+(i-1)h_n} \Delta X_{n,i}$ |
todo:
$\bullet$ filtered probability space (${F}_t$ being a filter meas with passing time, more and more of the algebra is available)
$\bullet$ adapted process ($X_t$ is measurable always w.r.t. the current ${F}_t$)
$\bullet$ limit in probability: $\left( {\mathrm{plim}}_{n \to \infty}X_n = X \right) \equiv \forall(\varepsilon>0).\ \lim_{n\to\infty}\Pr\left(d(X_n,X)\geq\varepsilon\right) = 0 $
where $\Pr\left(X\geq x\right) \equiv F_X(x)=\int_{-\infty}^xP_X(y)\,{\mathrm d}y $
and for a metric $d$ in a Separable space inducing a new random variable $d(X_n,X)$
(As $X_n,X$ isn't really in the domain of $d$, that's abuse of notation here)
$\bullet$ the sum can be done over other partitions of the interval $[a,b]$
The following definition corresponds to a sequence of equidistant grids. The common more general definition allows for more genial sequences of finer and finer grids.
Discussion
Note that for arbitrary $X_t$, the expressions $\Delta X_{n,i} = X_{a+ih_n}-X_{a+(i-1)h_n}$ are just a particular kind of stochastic processes. Importantly, it's one where the limit of $n$ to infto goes to zero (as a stochastic process). This is akin to $\Delta x_i$ going to zero in the Riemann integral, where $x(t)$ is some (non-stochastic) continuous function. Indeed for $X_t=x(t)$ a (deterministic) function, $\Delta X_i=x(a+ih)-x(a+(i-1)h)$ are just the lengths of parts of a grid-partitioning.
Comparison with other stochastic integrals
Trivially, $H_{a+(i-1)h}$ is
$\dfrac{1}{2}(H_{a+(i-1)h}+H_{a+(i-{\bf{1}})h})$.
If we shift the the index of the second term by one,
$\dfrac{1}{2}(H_{a+(i-1)h}+H_{a+(i-{\bf{0}})h})$,
we get another stochastic integral (Stratonowitsch-Integral).
In the case that we deal with smooth functions instead of stochastic processes, the discretization is irrelevant. Here, if $H$ and $X$ are correlated, this does make a difference.
Motivation
Math
For $p>0$, we have
$\int_\epsilon^1(p\,t^{p-1})\,{\mathrm d}t=\int_\epsilon^1{\mathrm d}t^p = 1-\epsilon^p$
and
$\lim_{\epsilon\to 0}\int_\epsilon^1(p\,t^{p-1})\,{\mathrm d}t = 1$
doesn't even depend on the value of $p$.
What's not so nice here is that the naive integral $\int_0^1(p\,t^{p-1})\,{\mathrm d}t$ doesn't exist for $p\in(0,1)$. This is because $\lim_{t\to 0}$ of e.g. $t^{\tfrac{1}{2}-1}=\tfrac{1}{\sqrt{t}}$ doesn't exist. We can also formulate that issue by saying that for $p\in(0,1)$, the function $t^p$ in $\int_\epsilon^1{\mathrm d}t^p$ isn't differentiable at $t=0$.
In conclusion,
“$\int_0^t{\mathrm d}\sqrt{s}=\sqrt{t}$”
doesn't make sense, only
$\lim_{\epsilon\to 0}\int_\epsilon^t{\mathrm d}\sqrt{s}=\sqrt{t}$
Physics
The accumulation of the values of a function $F$ along a smooth path x(t) is $\int_{t_0}^{t_1} F(x(s))\, {\mathrm d}x(s)$, which is $\int_{t_0}^{t_1} F(x(s))\, x'(s)\, {\mathrm d}s$, where
$x'(t)=\lim_{\Delta t\to 0}\frac{x(t+\Delta t)-x(t)}{\Delta t}$.
E.g. for $F$ being force, the integral along a path is the work.
The Itō integral is a limit of sums not over functions but stochastic processes, and there ${\mathrm d}{\mathcal W}_t$ doesn't rely on differential calculus. For ${\mathcal W}_t$ a Wiener process $\sqrt{\left\langle\left(\int_0^t {\mathrm d}{\mathcal W}_s\right)^2\right\rangle}=\sqrt{t}$.
In physics, the integral is a means of computing the accumulation of a function along a path in cases where $x'$ isn't defined in a sensible way. As the density associated with a random variable obtained by a stochastic integral follows a diffusion equation, those situations arise everywhere in the microscopic world, and many models in quantum mechanics look just like that as well.
QM
Consider the drift diffusion equation
$\frac{\partial}{\partial t}\psi=\mu\frac{\partial}{\partial x}\psi+\kappa^2\frac{\partial^2}{\partial x^2}\psi.$
Dimensional analysis tells us that $\mu$ is a characteristic length per time (drift velocity) while $\kappa$ is a characteristic length per square root of time. This small factoid has curious consequences.
In statistical physics, $\kappa^2=2D$ is the diffusion coefficient. What follows also applies to non relativistic quantum mechanics, except the diffusion coefficient is imaginary, $\kappa^2=\frac{i\hbar}{2m}$.
Example for how the situation arises
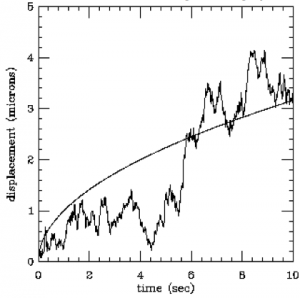 Given the value $x(t)$ of a curve/stochastic process at time $t$, for any time interval $\Delta t > 0$, we can test for $x(t+\Delta t)$ and the increment $\Delta x\equiv x(t+\Delta t)-x(t)$ is probabilistic and dependents on $\Delta t$ (and possibly on $t$ or even on $x(t)$).
For example, in the case of a Brownian motion each new $\Delta x$ takes values according to the distribution
Given the value $x(t)$ of a curve/stochastic process at time $t$, for any time interval $\Delta t > 0$, we can test for $x(t+\Delta t)$ and the increment $\Delta x\equiv x(t+\Delta t)-x(t)$ is probabilistic and dependents on $\Delta t$ (and possibly on $t$ or even on $x(t)$).
For example, in the case of a Brownian motion each new $\Delta x$ takes values according to the distribution
$P(\Delta x)=\dfrac{1}{\kappa\sqrt{\Delta t}\sqrt{2\pi}}\exp \left( -\dfrac{1}{2}\dfrac{(\Delta x)^2}{\kappa^2\,\Delta t} \right)$.
(I set $\mu=0$ and note that usually one uses a variable $\sigma=\kappa\sqrt{\Delta t}$)
The Gauss curve distribution for $\Delta x$ says that even for very small $\Delta t$, there is a non-vanishing change that $x(t+\Delta t)$ is far away from $x(t)$. For bigger $\Delta t$, the distribution flattens out and the chance for bigger net deviation grows.
Note that this weight also arises in the quantization of $L(q,{\dot q})\propto {\dot q}^2$: $\frac{(\Delta x)^2}{\Delta t}=\left(\frac{\Delta x}{\Delta t}\right)^2\Delta t\approx \int_0^{\Delta t} \left(\frac{{\mathrm d}x}{{\mathrm d}t}\right)^2{\mathrm d}t$
Now, for the above $P$, we have:
$\langle \Delta x\rangle=0$
$\langle \left|\Delta x\right| \rangle=\sqrt{\tfrac{2}{\pi}}\,\kappa\,\sqrt{\Delta t}$
$\langle (\Delta x)^2\rangle=\kappa^2\,\Delta t$
This says that the movement has no preferred direction, but for a finite waiting time $\Delta t$ and if $x(t)$ is some mean path, we expect $x(t+\Delta t)=x(t)+\kappa\sqrt{\Delta t}$, see picture. The intuition is that for a very small waiting time, you could possibly already have a big deviation and the longer the wait the farther you get away from the center - however this movement is sub-linear because with more time, more and more cancellation occur as well. The non-differentiability of the curve manifests itself here: While we know the overall deviation goes as $\sqrt{\Delta t}$, we can't make a good estimate for the instantaneous growth, because at $\Delta t=0$ the slope of the square root function isn’t finite! There is no $x'(t)$!
Itō process
An Itō process is a stochastic process $X_t$ which is the sums of a Lebesgue and an Itō integral:
$X_t = X_0 + \int_0^t \mu_s(X_s, s)\,\mathrm ds + \int_0^t \sigma_s(X_s, s) \,\mathrm dW_s$
One writes
${\mathrm d}X_t = \mu_t(X_t, t) \, {\mathrm d}t + \sigma_t(X_t, t) \, {\mathrm d}W_t$
If $X_t$ isn't known, this is called a stochastic differential equation in $X_t$. Being an Itō process is the stochastic analog of being differentiable.
If $\mu_t$ and $B_t$ are time independent, we speak of Itō diffusion.
A geometric Brownian motion is characterized via $\mu_t(X_s, s)=X_s\,\mu$ and $\sigma_t(X_s, s)=X_s\,\sigma$, i.e. both are “just” $\propto X_s$.
Itō lemma
${\mathrm d}f(t,X_t) = \left(\dfrac{\partial f}{\partial t} + \dfrac{\sigma_t^2}{2}\dfrac{\partial^2f}{\partial x^2}\right){\mathrm d}t + \dfrac{\partial f}{\partial x}\,{\mathrm d}X_t$
As this really is an integral relation, it corresponds to a version of the fundamental theorem of calculus. If we know how to integrate against $X_t$, we can compute $f(t,X_t)$ as such an integral (plus an ordinary integral).
See the references for a higher dimensional version of the lemma.
The following comment is foreplay to the next subsection: Note that for $f(x,t)=\frac{1}{2}x^2$ and $\frac{\sigma_t^2}{2}=\kappa^2$ we get
${\mathrm d}\left(\frac{m}{2}X_t^2\right) = m\,\kappa^2{\mathrm d}t + X_t\,m\,{\mathrm d}X_t$
Manifestation of the commutation relation
Let $p_{\Delta t}(t)=m\frac{x(t+{\Delta t})-x(t)}{{\Delta t}}$. If the limit $\lim_{\Delta t\to 0}p_{\Delta t}(t)$ exists, then for auxiliary $\delta$, we have $\lim_{\Delta t\to}x(t+\delta^2{\Delta t})=x(t)$.
Hence, for ever smaller time grid size ${\Delta t}$, e.g. an expression like $x(t+\delta_1^2{\Delta t})\,x(t+\delta_2^2{\Delta t})\,x(t+\delta_3^2{\Delta t})$ converges to $x(t)^3$.
However, for $x(t+\Delta t)\approx x(t)+\kappa{\sqrt{\Delta t}}$. We find $x(t+\delta^2{\Delta t})\,p_{\Delta t}(t)=\delta^4\,m\,\kappa^2+x(t)\,p_{\Delta t}(t)$.
The result says that two naively equivalent approximation schemes (e.g. $\delta=0$ vs. $\delta=1$) systematically differ by an additive diffusion term (e.g. $m\kappa^2$ here). I.e. the Itō integral is defined with most left of the grid cells as in the explicit Euler-method numerical approximation scheme. The implicit Euler-method simply corresponds to a different notion of integral here and would give a different result.
In quantum mechanics, the difference of the products
$[x,p]_{\Delta t}:=x(t+\delta^2{\Delta t})\,p_{\Delta t}(t)-x(t)\,p_{\Delta t}(t)$
equals $m\,\kappa^2=m\frac{i\hbar}{2m}=\frac{i\hbar}{2}$.
Fractional quantum mechanics
So we had
$\frac{\partial}{\partial t} \psi = \kappa^2 \frac{\partial^2}{\partial x^2} \psi$
(note the imbalance of dimensions, $t$ vs. $x^2$) and in turn
$P(\Delta x) \propto \exp\left(c\frac{(\Delta x)^2}{\Delta t}\right)$
as next-step distribution, and then $\langle |x|\rangle\propto t^{1/2}$ gives the non-smooth curve.
You may want to look at other next-step distributions, (effectively giving the theories with $\langle |x|\rangle\propto t^{1/\alpha}$) and this is all there is to „fractional quantum mechanics“. The imbalance $t$ vs. $x^\alpha$ for non-integer alphas forced fractional derivatives on you.
Reference
Wikipedia: Itō calculus, Itō lemma, Riemann–Stieltjes integral, Stratonovich integral, Path integral formulation, Fractional quantum mechanics
Stochastic Calculus Cheatsheet: http://furius.ca/cqfpub/doc/stocalc/stocalc.pdf