This is an old revision of the document!
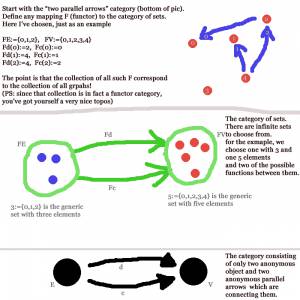
Functor category
Category
| context | ${\bf C}$ … small category |
| context | ${\bf D}$ … category |
| definiendum | ${\bf D}^{\bf C}$ in $\mathrm{it}$ |
| definition | $\mathrm{Ob}_{{\bf D}^{\bf C}}:={\bf C}\longrightarrow{\bf D} $ |
| definition | ${\bf D}^{\bf C}[F,G]:=F\xrightarrow{\bullet}G$ |
Idea
Algebraic picture if the target is structured
The nice target category ${\bf{Set}}$ is like a ring (say $\mathbb R$) and the functor category ${\bf{Set}}^{\bf{C}}$ with objects $\omega,\mu,\dots$ is like a space of functionals on a space ${\bf{C}}$. The topos/functional space is richer than the base ${\bf{C}}$: The target (${\bf{Set}}$ resp. $\mathbb C$) has a nice algebraic structure (e.g. co-products resp. addition), which we can pull back to define one on ${\bf{Set}}^{\bf{C}}$. As in $\omega+\lambda:=\left(v\mapsto\omega(v)+\mu(v)\right)$.
Adding more details leads to finer analogies: If $\mathbb C$ has co-products itself, then it's like a vector space and it's object should be viewed as a set of base vectors. If a functor preserves co-product, it's like a linear functional and ${\bf{Set}}^{\bf{C}}$ becomes a kind of dual vector space. This sheds light on the (co-variant) Yoneda embedding: If we view the objects of $\mathbb C$ as a set of base vectors, then the can be mapped to functionals in the dual space, but that space is bigger / also contains a lot of other functionals.
Remark: We don't necessarily need to take ${\bf{Set}}$ as target, although it's the traditional choice. It corresponds to the cardinal arithmetic (arbitrary cardinals). Meanwhile, the category of finite sets behaves like natural number (finite cardinals) and groupoids behave like reals (groupoid cardinality can be defined, where non-trivial automorphisms give fractional cardinality).
Example
Reference
Wikipedia: Functor category