This is an old revision of the document!
Hom-functor
Functor
| context | ${\bf C}$ … locally small category |
| context | $A:\mathrm{Ob}_{\bf C}$ |
| definiendum | $\mathrm{Hom}_{\bf C}(A,-)$ |
| inclusion | $\mathrm{Hom}_{\bf C}(A,-)$ in ${\bf C}\longrightarrow{\bf Set}$ |
| definition | $\mathrm{Hom}_{\bf C}(A,X):={\bf C}[A,X]$ |
| definition | $\mathrm{Hom}_{\bf C}(A,f):=g\mapsto f\circ g$ |
Discussion
Consider some objects $A$ and $X$ in the category ${\bf C}$, then ${\bf C}[A,X]$ is defined as the type of arrows from $A$ to $X$ (see the definitions in category theory). Given an arrow $f$ from $X$ to $Y$, there is a sensible induced arrow between types ${\bf C}[A,X]$ and ${\bf C}[A,Y]$, namely $g\mapsto f\circ g$.
If we are allowed to create new types as we please, then we could now create a category with objects being the types ${\bf C}[A,X], {\bf C}[A,Y],\dots$ and then use the above arrow mapping to define a functor “${\bf C}[A,-]$”. If ${\bf C}$ is locally small (which means ${\bf C}[A,B]$ can by viewed as a set), then, instead of creating such a new category, we just embed that structure in ${\bf Set}$. We denote the functor from ${\bf C}$ to ${\bf Set}$ by $\mathrm{Hom}(A,-)$.
Note that we write $\mathrm{Hom}(A,B)$ for what we'd usually write as $\mathrm{Hom}_{\bf C}(A,-)\,B$ and we similarly write $\mathrm{Hom}_{\bf C}(A,f)$ for $\mathrm{Hom}_{\bf C}(A,-)(f)$.
Contravariant hom-functor
Maybe I'll do a seperate entry later, although that's a little tiresome
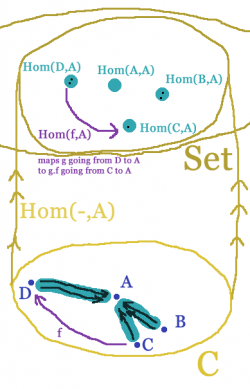
For all objects $A:\mathrm{Ob}_{\bf C}$, we define the functor $\mathrm{Hom}(-,A)$ with the obvious object mapping and the contravariant arrow mapping $g\mapsto g\circ f$. So an arrow $f$ from $X$ to $Y$ gets mapped to an arrow $\mathrm{Hom}_{\bf C}(f,B)$ between ${\bf C}[Y,A]$ and ${\bf C}[X,A]$.
The picture on the side shows how the functor $\mathrm{Hom}_{\bf C}(-,A)$ maps ${\bf C}$ into ${\bf Set}$.
Pontryagin duality
Here is an example where the image is of interest: Consider the object $U(1)$ in the category of locally compact abelian groups:
For any group $G$, the set $\mathrm{Hom}(G,U(1))$ inherits a group structure from $U(1)$, i.e. $S^1$ with multiplication $\cdot$. This is called the dual group and its elements are called “characters” $\chi$.
For example, consider $\mathbb R$ with addition. We'll see that this group is actually self-dual. Fix a real number $p$ and then e.g. $x\mapsto\mathrm{e}^{ipx}$ is an element $\chi_p$ of $\mathrm{Hom}(\mathbb R,U(1))$. It's a homomorphism, because $\mathrm{e}^{ipa}\cdot\mathrm{e}^{ipb}=\mathrm{e}^{ip(a+b)}$. We can use the multiplication of phases in $U(1)$ to define a group structure on these $\chi$'s by $\chi_p\bullet\chi_q\equiv(x\mapsto\mathrm{e}^{ipx})\bullet(x\mapsto\mathrm{e}^{iqx}):=x\mapsto\mathrm{e}^{i(p+q)x}$. We have a $\chi_p$ for all real numbers $p$ and so, in this case, as promised, we find $\mathrm{Hom}(\mathbb R,U(1))\cong\mathbb R$. As we'll see below, that “new” $\mathbb R$ from constructing the dual is the Fourier space!
Now since we see $\mathrm{Hom}(-,U(1))$ maps groups to groups, we can consider it as an auto-functor in the category of locally compact abelian groups. It turns out that the twice applied functor $\mathrm{Hom}(\mathrm{Hom}(-,U(1)),U(1))$ is naturally isomorphic to the identity functor. That's called the Pontryagin duality. The isomorphism is actually very simple to define: If $\chi\in\mathrm{Hom}(G,U(1))$, then we can map $g\in G$ to $g\mapsto\left(\chi\mapsto\chi(x)\right)$.
Since locally compact groups have the Haar measure, one can form the space of integrable functions $G\to\mathbb C$ and carry it along with these functors. This procedure is the Fourier transform and it really works for all groups in this category! E.g. for $U(1)$ itself, i.e. the periodic interval, we find that the dual group is $\mathbb Z$ and the associated transform is the Fourier series.
More general cases
- Extending this to a category of non-commutative groups is a research subject. Tannakian categories … Grothendieck stuff … we see that it's desirable for the Hom-sets to have their own algebraic structure (in the above, the Hom-set was again a group) and this is where many ideas come from.
- A similar construction works if we consider commutative Banach algebra and their maps maps to $\mathbb C$. This is the Gelfand transform business. It reduces to the Fourier transform if we consider the space $L^1(\mathbb R)$ and convolution as multiplication.
Yoneda
Motivation: The following is very similar to what we did with the maps to $U(1)$ above. Consider a vector space $\mathcal V$ over some field $\mathbb K$ (e.g. $\mathbb R^3$) and some functionals $\mu$ and $\nu$, which are elements of the function space ${\mathbb K}^{\mathcal V}$. We can defined their addition $\mu+'\nu$ by
$(\mu+'\nu)(v):=\mu(v)+\nu(v)$
simply because their values lie in the field $\mathbb K$, which already has addition. And as a side note, if we restrict ourselves to the linear functionals, then this functional space becomes the so called dual vector space.
Now back to the general case. Instead of working with the category ${\bf C}$, one can work with the category of set valued covariant functors ${\bf Set}^{{\bf C}^\mathrm{op}}$ (called Presheaf category). One substitutes an object $A$ with the contravariant functor $\mathrm{Hom}_{\bf C}(-,A)$ (=Yoneda embedding) and the arrows actually are the same/isomorphic to the old ones (=Yoneda lemma).
The advantage of this is that that new category ${\bf Set}^{{\bf C}^\mathrm{op}}$ has more objects than ${\bf C}$, namely some non-representable functors $F$. (Representable means $F$ is isomorphic to some hom-functor anyway.) For example, the category ${\bf C}$ might not have products $\times$, but because ${\bf Set}$ has products, the category ${\bf Set}^{{\bf C}^\mathrm{op}}$ always has them.
Reference
Wikipedia: Hom functor, Yoneda lemma