This is an old revision of the document!
KfV . note
Driver Assistent System Influence Model
Quantities of interest
- $n(t)$ … (measured, known) number accidents per year $t\in{\mathbb N}$
- $n^\mathrm{max}(t)$ … (unknown) number accidents that would happen without a particular driver assistant systems. As the system prevent some accidents, we have $n(t) < n^\mathrm{max}(t)$.
- $n_\mathrm{prev}(t) = n^\mathrm{max}(t) - n(t)$ … (unknown) number of accidents of $n^\mathrm{max}(t)$, that were prevented, resulting in $n(t)$
- $n_\mathrm{prev}^\mathrm{max}(t)$ … (unknown) number of accidents of $n^\mathrm{max}(t)$, that would be prevented if every car had implemented said system.
- $p := \dfrac{ n_\mathrm{prev}^\mathrm{max}(t) }{ n^\mathrm{max}(t) }$ … (guess, tested) potential of the system.
- $C(t)$ (known) number of cars on the street
- $C^*(t)$ (partially known) number of cars on the street that have implemented the assistance system. For each system, there was a time $t^*$ when when $C^*(t^*)=0$
- $x(t)=\dfrac{C^*(t)}{C(t)}$ … (partially known) distribution of the driver assistance system.
- $p^\mathrm{eff}(t) := \dfrac{ n_\mathrm{prev}(t) }{ n^\mathrm{max}(t) }$ … (unknown) effective potential of the system.
Mitigation and Worsening
Let
$M(t)=1-p^\mathrm{eff}$
We have
$M(t)\,n^\mathrm{max}(t) = \left(1-\dfrac{ n_\mathrm{prev}(t) }{ n^\mathrm{max}(t) }\right)n^\mathrm{max}(t) = n^\mathrm{max} - n_\mathrm{prev}(t) = n(t)$
Thus $M(t)$ represents the mitigation factor, taking the worse case number of accidents $n^\mathrm{max}(t)$ to the real number $n(t)$. Furthermore, let
$W(t) := \dfrac{1}{M(t)} = \dfrac{1}{1-p^\mathrm{eff}}$
denote the worsening factor, so that
$W(t)\, n(t) = n^\mathrm{max}(t)$
As $n(t)$ can be empirically available, evaluation of $W(t)$ will be more relevant than of $M(t)$.
The simplest model for p^eff
The distribution $x(t)\le 1$ affects the effective potential. W.r.o.g., we may let
$p^\mathrm{eff} = \Sigma(t)\,x(t)\,p$
where $\Sigma(t)\in(0,1)$ captures all other effects that negatively effect the effective potential. In the following, we'll assume the reduced distribution is the only reason for a reduced potential, i.edeviation(t)=1$. Thus
$W(t) := \dfrac{1}{1-x(t)\,p}$
Using the geometric series $\frac{1}{1-z}=\sum_{k=0}z^k$, we may look at an approximation
$W(t) \approx 1 + x(t)\,p + \left(x(t)\,p\right)^2 $
We can furthermore consider the expansion of the $W(t)$ in $t$ at $t^*$, where $x(t^*)=0$.
$W(t) \approx 1+x'(t^*)\,p\,(t-t^*)+\left(1+\beta\right)\cdot\left(x'(t^*)\,p\,(t-t^*)\right)^2$
with
$\beta=\dfrac{1}{2}\dfrac{1}{p}\dfrac{x''(t^*)}{x'(t^*)}$
Linear distribution model
In the following, let the distribution $d$ be known/measured to have the values $x^{**}$ at a time $t^{**}$. Define a linear transformation
$s(t)=\dfrac{t-t^*}{t^{**}-t^*}$,
It's chosen so that $s=0$ correspond to the introduction and $s=1$ to the evaluation of the distribution.
The linear model for $d$ reads
$x(t)=\begin{cases} 0 &\hspace{.5cm} \mathrm{if} \hspace{.5cm} t<t^* \\\\ x^{**}s(t)\hspace{.5cm} &\hspace{.5cm} \mathrm{else} \end{cases}$
However, note that as a distribution with $x(t)\le 1$, for $t>t^{**}$ the approximation must somehow start to become flat. This is improved on below.
As $x''(t)=0$ and thus $\beta=0$ for a second order expansion of $W(t)$ above, we get
$W(t) \approx 1 + p\,x^{**}\,s(t) + (p\,x^{**}\,s(t))^2$
Systems of driver assistance systems
Consider now a whole set of systems indexed by $I=\{\mathrm{FAS}_1, \mathrm{FAS}_2,\dots,\mathrm{FAS}_m\}$
Assuming no two systems correlate, we get
$W(t)=\prod_{i=1}^m\dfrac{1}{1-x_i(t)\,p_i}$
Let's look at a systems that shares the times $t^*$ and $t^{**}$. If we consider the linear approximations for $x_i(t)$, we can get the closed form series expression
$W(t)=\sum_{k=0}^\infty b_k s(t)^k$
where
$b_0=1$
$b_1=\sum_{i=1}^mp_i$
$b_2=\sum_{i\le j}^mp_ip_j$
$b_3=\sum_{i\le j < k}^mp_ip_jp_k$
etc.
Proof scetch by induction:
$\dfrac{1}{1-x}=1+x+x^2+\dots$
$\dfrac{1}{1-x}\dfrac{1}{1-y}=(1+x+x^2+\dots)\cdot(1+y+y^2+\dots)=1+(x+y)+(x^2+xy+y^2)+\dots$
$\dfrac{1}{1-x}\dfrac{1}{1-y}\dfrac{1}{1-z}=(1+(x+y)+(x^2+xy+y^2)+\dots)\cdot(1+z+z^2+\dots)=\dots$
etc.
Time evolution of the system distribution
Warmup: The logistic differential equation
$x'(t) = k \cdot x(t) \, \left( K - x(t) \right)$
is e.g used to model the growth of bacteria density $x(t)$ where there's a maximal capacity $x(\infty)=K$. The proportionality factor $k \cdot x(t)$ says the grows is proportional to what's already there and the second factor $K - x(t)$ makes sure $x(t)$ can't grow beyond $K$. The solutions become flat at infinity, but the initial growth is also starting at minus infinity. For normed distributions, $K=1$.
A more realistic class of models for the distribution of assistance systems, that combines the constant (zero) initial value, then an initial linear growth (unlike the logistic function) and a slow flattening, appears to be
$x(t)=x^*$ for $t\le t^*$.
$x'(t)=A(t)\,(1-x(t-t^*))^{1-q}$ for $t> t^*$
for some real $q$. The function $A(t)$ maybe represents the product attractiveness of the system and $1-x(t-t^*)$ are the fraction of drivers at $t-t^*$ which haven't implemented the system product. The equation makes senses in as far as only those drivers can make the distribution of $d$ grow (and there is no reproduction that would depend on the existing distribution $x(t)$, as in the logistic model).
At the introduction of the system, this model makes for a linear rise for small $t>t^*$ and a flattening $x'(\infty)=0$.
We will assume a constant attractiveness $A$. The differential equation is solved by
$x(t)=1-\left((1-x^*)^q-q\,A\cdot(t-t^*)\right)^\frac{1}{q}$
We'll take a look at the model with $q\mapsto 0$, in which case we have
$x(t)=1-(1-x^*)\,{\mathrm e}^{-A\cdot(t-t^*)}$
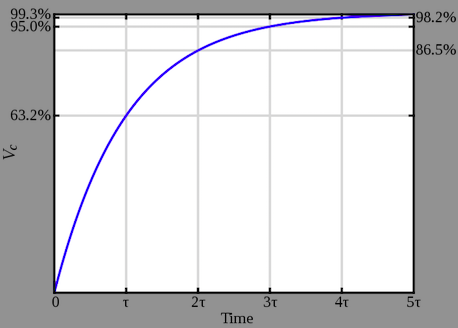
This is the same functional behavior as as resistor voltage step-response in an RL circuit. The linearization for small $t>t^*$ equals
$x(t)\approx x^* + A(t^*)\cdot(t-t^*)$.
Second boundary condition
If $x(t^{**})=x^{**}$, then
$A=\dfrac{1}{t^{**}-t^*}\log\left(\dfrac{1-x^*}{1-x^{**}}\right)\approx\dfrac{1}{1-x^*}\dfrac{x^{**}-x^*}{t^{**}-t^*}$
and
$x(t)=1-(1-x^*)\left(\dfrac{1-x^{**}}{1-x^*}\right)^{s(t)}$
Indeed, for this function
$x(t^*)=1-(1-x^*)\cdot 1=x^*$
$x(t^{**})=1-(1-x^*)\dfrac{1-x^{**}}{1-x^*}=x^{**}$.
Example for $t^*=2$ and $x^*=0$, $t^{**}=5$ and $x^{**}=0.7$:
https://www.wolframalpha.com/input/?i=1+-+(1+-+0.7)%5E((t+-+2)%2F(5+-+2))+from+0+to+10
For assistance systems
We will always have $x^*=0$, as a system can't have any effective potential before it's introduced, so
$x(t) = 1-(1-x^{**})^{s(t)}$
Thus
$W(t) := \dfrac{1}{1-x(t)\,p} = \dfrac{1}{1 - p + (1-x^{**})^{s(t)} p} = L + R$
which splits into the the know linear second order expansion
$L = 1 + p\,x^{**}\,s(t) + (p\,x^{**}\,s(t))^2$
and then some other nonlinear correction terms
$ R \approx (x^{**})^2 \,p\,\left((-p+\frac{1}{2}s)+(p-\frac{1}{2})s^2\right)+\dots$
(At this point the evaluation of the expansion will be more computationally expensiive than using the exact formula with the fraction and exponentials above.)
Summary
The presented model predicts that given a maximal potential $p$ for a system introduced at $t^*$ and with a distribution $x^{**}$ at $t^{**}$, the mitigation factor for $t\ge t^*$ giving the relation
$n^\mathrm{max}(t)\,M(t) = n(t)$
is given by
$M(t) = 1 - p + (1-x^{**})^{s(t)} p$
where
$s(t)=\dfrac{t-t^*}{t^{**}-t^*}$
is a linear function. As should be, we have that
$M(t\le t^*) = M(t^*) = 1-\left(1-\left(1-x^{**}\right)^{0}\right)p = 1$
$M(t^{**}) = 1-\left(1-\left(1-x^{**}\right)^1\right)p = 1 - x^{**}\,p$
$M(\infty) = 1-\left(1-0\right)p = 1-p $
Given the above data, the worsening $W(t):=\dfrac{1}{M(t)}$ can be used estimate a would be scenario from empirical accident data $n(t)$.
Stochastic deviation
We considered $p^\mathrm{eff}(t)=x(t)\,\Sigma(t)\,p$. Unknown effects $\Sigma(t)$ may be included in form of a stochastic deviation around the car distribution. We'll introduce a term $\propto\sigma\,{\mathcal W}_t$ to the time evolution of $p^\mathrm{eff}(t)$, where $\sigma$ is a positive real parameter, ${\mathcal W}_t$ a Wiener process and we must do it in such a way that $x(t)\,\Sigma(t)\in[0,1]$.
To this end we take the differential equation
$x'(t) = A\,(1-x(t))$
i.e.
${\mathrm d}x(t) = A\,(1-x(t))\,{\mathrm d}t$
with
$A=-\dfrac{1}{t^{**}-t^*}\log(1-x^{**})$
to
${\mathrm d}X_t = A\,\left[(1-X_t)\,{\mathrm d}t+\sigma\,(4\,X_t\,(1-X_t))^r\,{\mathrm d}{\mathcal W}_t\right]$
with e.g. $r=\frac{1}{2}$.
A expression $4\,X_t\,(1-X_t)\in[0,1]$ is a variation of the stochastic term of the Cox–Ingersoll–Ross-like differential equation (I added a quadratic factor in the distribution with the stochastic term so that it never exceeds $d=1$).
This turns the worsening
$W_t=\dfrac{1}{1-X_t\,p}$
into a stochastic processes. (Or rather a family of such processes, parametrized by $\sigma$ and the standard deviation of the Wiener process.)
For related information, see the simpler Ornstein–Uhlenbeck process with the solution
$X_{t-t^*} = 1-\exp(-A\,(t-t^*)) + \sigma\, {\mathrm e}^{-A\,(t-t^*)}\int_{t^*}^t{\mathrm e}^{+A\,(s-t^*)}\,{\mathrm d}{\mathcal W}_{t^*-s}$
https://en.wikipedia.org/wiki/Ornstein%E2%80%93Uhlenbeck_process)
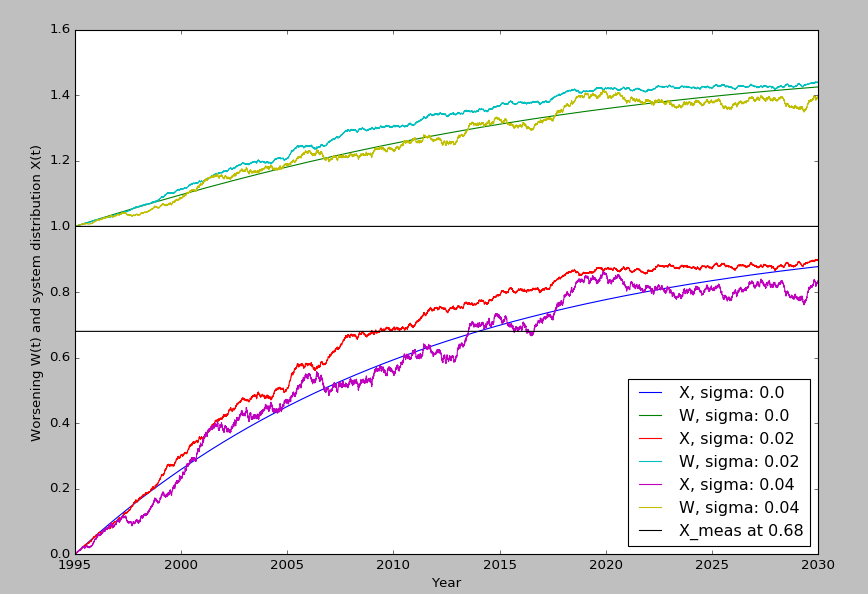
Example: Prediction for the ESP system
Here we have data for the ESP system, with a distribution of $x^{**}=0.68$ in the year 2014 and thus a slope $A\approx 0.0326$ according to the formula above.
With an estimated (maximal) death reduction potential of $p = 0.34$, the ESP system is the one with the highest $p$ in the list. If all cars had it implemented, $34\%$ of potential deaths would be prevented. In other words, the worsening is $1/(1-0.34)=1.\dot{5}\dot{1}$, meaning if it was never introduced, there would be about $150\%$ as many deaths at this late time. Indeed, removing $34\%$ or those $150\%$ leaves us with the actual $100\%$. Therefore, in the model, we have a stochastic process eventually ending in $X_\infty=1.\dot{5}\dot{1}$. (This is something a linear, without arbitrary cutoff, can't be consistent with.)
The second horizontal line is drawn at $x^{**}$, which intercepts with the $\sigma=0$ curve at $t=2014$. This model still assumes the car distribution eventually reaches 1. The stochastic differential equation, and thus the whole model, can easily be modified to tend towards a maximum $x^\infty<1$ by replacing both expressions $1 - X_t$ with $x^\infty - X_t$.
In the following image, we compute $X_t$ and the associated $W_t$ for $\sigma\in \{0, \frac{1}{100}, \frac{4}{100}\}$ (=$\{0, 0.3, 0.7\}$ after a reparametrization wednesday night). The stochastic variation is implemented via monthly fluctuation, making for $35{\cdot}12$ jumps. The standard deviation of the Wiener process is chosen to be $1$.
code implementation
import numpy as np import matplotlib.pyplot as plt p = 0.34 t_intr = 1995 t_meas = 2014 X_meas = 0.68 A = - np.log(1-X_meas) / (t_meas - t_intr) # equals 0.0326.. r = 1.0 / 2 # small r means smaller penalty on the sides of X=1/2 sigma_Wiener = 1.0 sigmas = [0.00, 0.3, 0.7] jumps_per_year = 12 t_star = t_intr t_stop = 2030 N = (t_stop - t_star) * jumps_per_year dt = (t_stop - t_star) / float(N) t = np.arange(t_star, t_stop, dt) X = np.zeros(N) W = np.ones(N) for sigma in sigmas: for i in xrange(1, t.size): capac = 1 - X[i-1] fluct = sigma * (4 * X[i-1] * capac)**r dW = np.random.normal(loc = 0.0, scale = sigma_Wiener) * np.sqrt(dt) X[i] = X[i-1] + A * (capac * dt + fluct * dW) W[i] = 1 / (1 - p * X[i]) plt.plot(t, X, label = "X, sigma: " + str(sigma)) plt.plot(t, W, label = "W, sigma: " + str(sigma)) plt.plot(t, np.ones(N), color = 'k') plt.plot(t, np.ones(N) * X_meas, color = 'k', label = "X_meas at " + str(X_meas)) plt.ylabel("Worsening W(t) and system distribution X(t)") plt.xlabel("Year") plt.legend(loc = 4) plt.show()