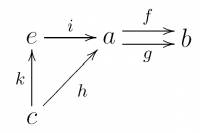Equalizer . category theory
Tuple
| context | $F:(a{\overset{\rightarrow}{\rightarrow}}b)\longrightarrow{\bf C}$ |
| definition | $\langle E,\langle Fa\mapsto e,Fb\mapsto e'\rangle\rangle := \mathrm{lim}\,F$ |
Here $a{\overset{\rightarrow}{\rightarrow}}b$ denotes the two object category with two parallel arrows.
Let $A:=Fa$, $B:=Fb$ and $f$ be one of the fmap images. Then $e:{\bf C}[E,A]$ and the other arrow must be $e\circ f$ and is hence usually ignored.
Examples
In ${\bf{Set}}$, if $f,g:A\to B$, then their equalizer is the set
$E=\{a\in A\ |\ f(a)=g(a)\}$
and $e:E\to A$ is the obvious injection.
Remark: In the image, $e=E$ and $i=e$.