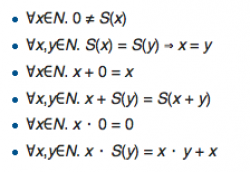Babbys first HoTT
Note
Curry-Howard correspondence and geometric semantics
| syntax | computation | logic | geometry |
|---|---|---|---|
| $P$ | type | proposition | space |
| $x$ with $x:P$ | term $x$ of type $P$ | argument $x$ for proposition $P$ | point $x$ of $P$ |
| $\bf{0}$ | empty type | false proposition | empty set |
| ${\bf 1}$ | type which does have one unique term | true proposition | singleton |
| ${\bf 2}$ | Bool | true proposition$^\star$ | set with two points |
$^\star$Some type theories make any type into a proposition and any proposition into a type and a proposition is true iff we can construct some term of the corresponding type. HoTT is a type theory where only some types are propositions, namely those who have up to one unique term, see below.
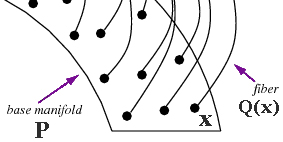
For $x:P$, consider a well formed expression $Q(x)$. This can be viewed as an $x$-parametrized family of types, a predicate with an open variable from, or a collection of fibres over a base.
| syntax | computation | logic | geometry |
|---|---|---|---|
| ${\large{\prod}}_{x:P} Q(x)$ | type of functions $s$ mapping an $x$ into $Q(x)$ | $\forall (x\in P).\,Q(x)$ | sections |
| ${\large{\sum}}_{x:P} Q(x)$ | type of pairs $\langle x,y\rangle$ with $x:P$ and $y:Q(x)$ | $\exists (x\in P).\,Q(x)$ | total space |
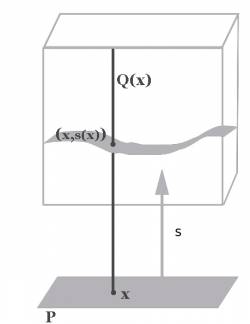
Constructing a term $s:{\large{\prod}}_{x:P} Q(x)$ is finding an argument $s$ for $\forall (x\in P).\,Q(x)$. The latter means being able to translate any argument $x$ for $P$ into an argument $s(x)$ of $Q(x)$. This is a functional assignment corresponding to a section of a fibration. The sum type works analogously.
If $Q$ is free of $x$, we can define implication $\implies$ and conjunction $\land$ as special cases of the above:
$P\to Q \equiv {\large{\prod}}_{x:P} Q$
$P\times Q \equiv {\large{\sum}}_{x:P} Q$
If we tag the terms of a type $P$ resp. $Q$ with the value of Bool, we can identify disjunction $\lor$ as $P+Q\equiv{\large{\sum}}_{x:{\bf 2}}\dots$ where the dots represent a suitable $if$-construction. Negation $\neg P$ is read as $P$ leading to absurum, i.e. $P\to{\bf 0}$. And lastly
| syntax | computation | logic | geometry |
|---|---|---|---|
| $P'$ with $P'<:P$ | subtype | implied propositions | subspace |
We have, for all $P$, a poset of types/propositions/spaces, with ${\bf 1}$ the maximum (by definition, we know the term of ${\bf 1}$ and hence, given a term of ${\bf 1}\to P$, we obtain one of $P$).
Identity type
We saw how a predicate logic can be expressed as type theory. When this is extended to equalitarian logics, we deal with Intentional type theory alla Per Martin-Löf. Here, for any type $P$, we get an identity type $=_P:P\to P\to\mathrm{Type}$. It must be defined in a way which respects symmetry and substitution, which implies transitivity, reflexivity etc.
Example 1
For example, we can specify the theory of semigroup as
$Semigroup\equiv{\large{\sum}}_{A:\mathrm{Type}}{\large{\sum}}_{m:A\to A\to A}{\large{\prod}}_{x:A}{\large{\prod}}_{y:A}{\large{\prod}}_{z:A}\ m(x,m(y,z))=_A m(m(x,y),z)$
A term of $SemiGroupStr$ is a pair $\langle A,\langle m,p\rangle\rangle$, where the first entry is a type $A$ and the second entry is pair, where the first entry is a function $m:A\to A\to A$ and the second entry is a proof $p$ that this $m$ fulfills the usual axiom. We do constructive mathematics here, so $p$ is a function which takes any $x$ to a function which takes any $y$ to a … to a function which takes any $m(m(x,y),z)$ to a term which demonstrates the required equality.
Example 2
As another example (which incidentally is also a semigroup, but that's not the point here) we can inductively define the natural numbers $\mathbb N$ as type by postulating
$0:\mathbb N$
and
$S:\mathbb N\to \mathbb N$.
Now
$0,S0,SS0,SSS0,\dots$
are all terms of $\mathbb N$. The picture on the right shows arithmetic alla Peano in first order logic
Using the 3rd and 4th axioms we can define an addition function $+:\mathbb N\to\mathbb N\to\mathbb N$, which we denote as $plus$ here, as
$plus(n,0):=n$
$plus(n,Sm):=S(plus(n,m))$
Using the 1st and 2nd we can define an identity type $=_\mathbb N:\mathbb N\to\mathbb N\to\mathrm{Type}$, which denote as $Code$ here, as
$Code(Sn,0)\ :=\ {\bf 0}$
$Code(0,Sm)\ :=\ {\bf 0}$
$Code(Sn,Sm)\ :=\ Code(n,m)$
$Code(0,0)\ :=\ {\bf 1}$
For any $n,m$, the above identity type $n=_\mathbb{N}m$ is defined in a way so that its either ${\bf 0}$ or ${\bf 1}$. So it either has a term or not, and under Curry-Howard the former means it's false and the latter means it's true. The dependent type $=_\mathbb{N}$ is equivalent to a binary predicate or a function of type $\mathbb N\to\mathbb N\to\mathbb {\bf 2}$ but to consider it a map into $\mathrm{Type}$ becomes important in the following.
There are a million ways to define and work with equality. For example, depending on the theory you treats functions intentional or extenional, the function mapping $n$ to $2(n+5)$ and the function mapping $n$ to $2n+10$ might be judged to be different or the same. For example, the former theory might be suited to study the difference between sorting algorithms (which do the same job, but possibly need different number of computing steps), while the latter may not. Intensional theories also have better decidablity properties regarding type checking but, as one can imagine, they are also much more complicated to work with.
We now turn to a variation of intentional type theory with an additional axiom which implies function extensionality.
Homotopy type theory
The following statements relating to the above construction are fairly clear: The type $Code(n,m)$ reduces to the same type as $Code(m,n)$. If $Code(n,k)$ and $Code(k,m)$ reduces to ${\bf 1}$, then so does $Code(n,m)$. That $Code(0,0)$ has a known term follows from the reflexivity property.
Abstractly, the rules for identity constructively say that if $p:x=_Py$, then there is a term $i(p):y=_Px$, if further $q:y=_Pz$, then there is a term $t(p,q):x=_Pz$, and for any $x$, there is a trivial term $refl_x:x=_Px$. Note that nothing holds us from defining identity types with more than one term.
Motivated by this, homotopy type theory generally defines identity types $x=_Py$ as path spaces where the above functions are given by inversion $p^{-1}$, concatenation $p\circ q$ and constant path. Path spaces also behave like hom-classes $\mathrm{Hom}_P[x,y]$ of groupoids (categoris where everything is invertible) and in fact, since terms $p,q:x=_Py$ of an identity type can also be compared for identity via $p=_{x=_Py}q$, we deal with homotopies or higher categories.
Example
We can inductively define the circle $\mathbb S$ as type by postulating $base:\mathbb S$ and $loop:base=_{\mathbb S}base$. Now $\dots,loop^{-2},loop^{-1},refl_{base},loop,loop^2,loop^3,\dots$ are all terms of $base=_{\mathbb S}base$. This type can be shown to be equivalent (in the formal sense discussed below) to the integers. Indeed, recall that the first homotopy group of the circle is isomorphic to $\mathbb Z$.
The above construction is synthetic in the sense Euclid writes down geometry. This is in contrast to a Cartesian approach, where we define the circle analytically as a set of points.
Propositions and sets
In this framework, not all types are sets, proposition or either of those. The following identifications are made:
- We say a type is a proposition iff its boolean, i.e. if it either has no term, or one unique term. This can be characterized as saying that all terms must be the same
$isProp(A):={\large{\prod}}_{x:A}{\large{\prod}}_{y:A}\,x=y$
Recall that for any $n,m:\mathbb N$, we could code up $n=_\mathbb{N}m$ in a way so that it's either ${\bf 0}$ or ${\bf 1}$.
- We say a type is a set iff $x=y$ is a proposition.
$isSet(A):={\large{\prod}}_{x:A}{\large{\prod}}_{y:A}\,isProp(x=y)$
The above says that $x$ connects to $y$ via at most one invertible path and hence this characterizes as set as a discrete category. Since sets, characterized like here as types with lack of other structure, are generally different from sets characterized in a theory like ZFC.
Homotopy theory
The general point here is that when path spaces already come together with the simple logical notion of equality, we can do a lot of geometry in the native language of the theory. We can define geometric quite directly. E.g. for any $\pi:A\to B$ and $b:B$, the type ${\large{\sum}}_{x:A}\, \pi(x)=b$ is a collection of $x's$ together with demonstrations that $\pi(x)=b$, i.e. the $x$'s are values in a fibre over $A$. You can express that a space is contractible (shrinkable to one point) by using $isProp$ and you can in turn use this to express homotopy for functions and then homotopy equivalence $\simeq$ of spaces. The univalence axiom of homotopy type theory finally says that you should generally view a type as homotopy type of a space (that naming overlap is a happy coincidence) and accordingly guarantees a term of the type
$(A\simeq B)\to (A=B)$
converting any homotopy to an argument for equality.
Some more curious identifications: If $f$ is a function, then $x=_Ay$ implies $f(x)=f(y)$. Constructively, this means we can lift a path $p:x=_Ay$ to a path $p_*:f(x)=f(y)$. This makes any function into a functor with $\mathrm{fmap}\ p:=p_*$. Moreover, the condition for $H$ to be a homotopy between two functions is exactly the one of being a natural transformation.
Internal logic of a cateogry and models
Now if we read $P:\mathrm{Ob}_{\bf C}$ as types, then an arrow $\pi:{\bf C}[Q,P]$, viewed as a projection map for a fibre bundle, defines fibres and hence a dependent type ${\large{\prod}}_{x:P} Q(x)$. If ${\bf C}$ is a topos, then we have subobjects, i.e. subspaces.
In this way a) each category itself provides a syntactic framework b) categories provide models for type theories. For example, simply typed lambda calculus corresponds to Cartesian closed categories (it has function spaces as objects etc.) and homotopy type theory corresponds to some wild higher topos.
Here's how to semantically caputure identity types/path spaces:
Generally, if $\pi:E\to B$ is a map and $b:B$, then $F(b):=\pi^{-1}(b)$ is a fibre.
As a special case, let $I$ by some sort of interval so that $B^I\equiv I\to B$ is the space of paths. Then $\pi:B^I\to (B\times B)$ gives us, for each $\langle b_{start},b_{end}\rangle:B\times B$ a space of paths $Path(b_{start},b_{end}):=\pi^{-1}(\langle b_{start},b_{end}\rangle)$.
(Another note: Roughly, in topos theory the dependent product “$S=\prod_{x:B}p^{-1}(x)$” w.r.t. an arrow $p:E\to B$ can be captured (I put the expression in quotes because we don't really have arguments $x$ when we don't deal with sets/types), as the object so that $p\circ eval=\pi$, were $eval:S\times B\to B$. See the hard to read article dependent product.)
Reference
Wikipedia: Homotopy type theory
homotopytypetheory.org: HoTT Book
nLab: internal logic, dependent product
todo