Hausdorff space
Set
| definiendum | $\langle X,\mathcal{T}_X\rangle \in\mathrm{it} $ |
| inclusion | $\langle X,\mathcal{T}_X\rangle$ … topological space |
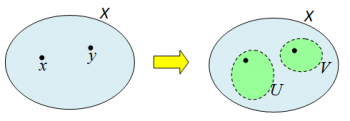
| for all | $x,y\in X, x\ne y$ |
| exists | $U_x\in$ Neighbourhood$(\mathcal{T}_X,x)$, $V_y\in$ Neighbourhood$(\mathcal{T}_X,y)$ |
| postulate | $U_x\cap V_y=\emptyset$ |
Discussion
Idea
A Hausdorff space $\langle X,\mathcal{T}_X\rangle$ is one where the topology $\mathcal{T}_X$ is fine enough so that separate points also have seperate neighbourhoods.
Also, boobs.
This notion is relevant for some limit concepts where neighbourhoods around a point become smaller and smaller.
Examples
Any metric space.
Non-examples
An ordered set like $\mathbb R$ and the right-ordered topology, i.e. the “infinite to the right” sets ${x\|\ x>a}$. Here a neighbourhood of $3$ can not be small enough to not contain the number $7$.
Reference
Wikipedia: Neighbourhood
Parents
Subset of
Requirements
