k-tape Turing machine
Set
| context | $ k\in\mathbb N $ |
| definiendum | $ \langle Q,\Gamma,\Sigma,\delta\rangle \in \mathrm{TM}_k $ |
| inclusion | $ \Sigma\subset\Gamma$ |
| inclusion | $ \delta: Q\times\Gamma^k \to Q \times \Gamma^k \times \{\mathrm{L},\mathrm{S},\mathrm{R}\}^k$ |
| postulate | $ q_\mathrm{start},q_\mathrm{halt}\in Q $ |
| postulate | $ \Box,\triangleright,0,1\in\Gamma $ |
| postulate | $ \Box\notin\Sigma $ |
Discussion
Let's discuss the 1-tape Turing machine, i.e. $k=1$. The general case is then clear.
A Turing machine $M\equiv\langle Q,\Gamma,\Sigma,\delta\rangle$ in $\mathrm{TM}_1$ is interpreted to encode how to walk along a tape of symbols and also write on it. The set $\Gamma=\{\Box,\triangleright,0,1,\dots\}$ is an alphabet of characters, the subset $\Sigma$ of it is the legal input alphabet, $Q$ is called a set of states and and $\delta$ is called the transition function. Here is how it goes: Starting the machine, we imagine an infinite string of characters
$ \triangleright\ \underset{q_\mathrm{start}}{a}\ b\ c\ d\ \cdots\ v\ w\ x\ y\ z\ \Box\ \Box\ \Box\ \Box\ \Box\ \cdots $
The input is the data between $\triangleright$ and the first $\Box$ and can be any word in $\Sigma^*$. The so called writer head starts out at the first input character in the state $q_\mathrm{start}$. Now for each given configuration, the transition function $\delta$ tells us how to get to the next one. Depeding on the state $q_j\in Q$ we are in, the $\delta$-component for “$\Gamma\to\Gamma$” tells us what how to overwrite the character at the writer head. And then the last component “$\to\{\mathrm{L},\mathrm{S},\mathrm{R}\}$” puts out the an left/stay/right-information and hence tells us where which place to move the head next. Let's denote the statement “The machine is currently in the state $q_j$ with the tape reading $\triangleright\ a\ b\ c\ d\ \cdots $ and writer head over $b$” by
$ \triangleright\ a\ \underset{q_j}{b}\ c\ d\ \cdots $
If the transition function on $\langle q_j,b\rangle$ evaluates as $\delta(q_j,b)=\langle q_k,x,\mathrm{R}\rangle$ then we interpret this as the instruction.
$ {\triangleright\ a\ \underset{q_j}{b}\ c\ d\ \cdots}\hspace{.2cm} \mapsto \hspace{.2cm}{\triangleright\ a\ x\ \underset{q_k}{c}\ d\ \cdots} $
The simulation is over when the state reaches $q_\mathrm{halt}$.
As a remark, one can reconstruct all of $\langle Q,\Gamma,\Sigma,\delta\rangle$ from $\delta$ along. Moreover, for any Turing machine, one can find another one with uses the reduced alphabet $\Gamma=\{\Box,\triangleright,0,1\}$. However, the latter compressed version runs longer, as is discussed in the Theorem section.
Notation
We write $\mathrm{TM}\equiv\mathrm{TM}_1$.
Example
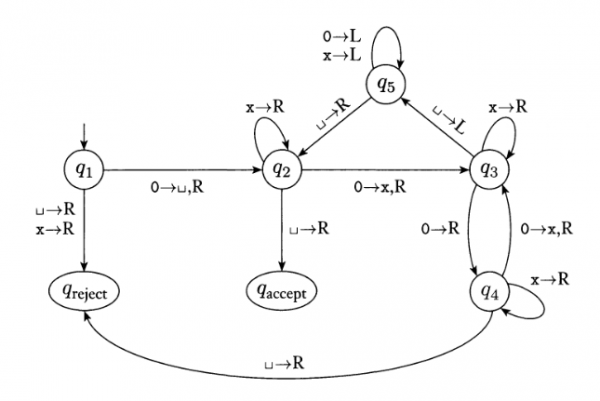
The following sucker lets you compute if your input is a string of 0's of length $2^n$ for some $n$. The picture encodes $\delta$ and $\triangleright$.
The conventions in the pic (Snipsers book) are slightly different, blanks are denoted by another symbol, $q_\mathrm{start}$ is $q_1$, there are two final states $q_\mathrm{accept},q_\mathrm{reject}$ instead of $q_\mathrm{halt}$ and $\mathrm{x}$ is used for what we would likely use $1$. The simulation is considered over when $\delta$ doesn't tell you anymore what to do.
For example, for the input “$0000$” we get
- $ \triangleright\ \underset{q_1}{0}\ 0\ 0\ 0\ \Box\ \Box\ \cdots $
- $ \triangleright\ \Box\ \underset{q_2}{0}\ 0\ 0\ \Box\ \Box\ \cdots $
- $ \triangleright\ \Box\ \mathrm{x}\ \underset{q_3}{0}\ 0\ \Box\ \Box\ \cdots $
- $ \triangleright\ \Box\ \mathrm{x}\ 0\ \underset{q_4}{0}\ \Box\ \Box\ \cdots $
- $ \cdots$
Theorems
In the entry Turing machine as partial function I formally define the runtime of a Turing machine $M\in\mathrm{TM}$ and what it means to say a Turing machine computes a function in $T(n)$-times. There I discuss effects of variation of tape-number or alphabet size on runtime. Here some similar remarks on variants of the above Turing machine concept:
For any Turing machine one can find an alternative oblivious Turing machine, which principally works the same, but where the heads movements don't depend on the tape content but are predetermined in advance for all inputs. For 2-tape Turing machines, using such an alternative also results in an logarithmic overhead.
Switching to a tape which is infinite in both directions gives a runtime bonus factor of $\frac{1}{4}$. Other variations are two- or three dimensional tapes and random access (larger head movements at a single step), but they don't have a significant effect on runtime neither.
See also Universal Turing machine.