Limit . category theory
Collection
| context | $F:{\bf C}^{\bf D}$ |
| context | $\Delta:{\bf C}\longrightarrow{\bf C}^{\bf D}$ … diagonal functor |
| definiendum | $\mathrm{lim}\,F$ … terminal morphism from $\Delta$ to $F$ |
Elaboration
A limit of a functor with image in ${\bf C}$, if it exists, is a particular terminal morphism in the functor category ${\bf C}^{\bf D}$. That definition emphasizes the underlying universal property, but it's a little hard to understand what's really going on. The reason is that a morphisms in a functor category is a natural transformation and this means there are a couple algebraic identities which don't get explicitly mentioned in the definition above. If you don't know limits, skip the next section and read the ones using cones first.
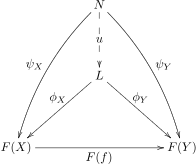
Firstly, keep in mind that in a functor category ${\bf C}^{\bf D}$, the main data of a terminal morphism to $F\in {\bf C}^{\bf D}$ is a natural transformation $\phi$ from some functor to $F$. Loads of other natural transformations factor through this $\phi$.
We now restate the above definition using a little more prose: The diagonal functor $\Delta$ maps an object $N$ in ${\bf C}$ to a pretty degenerate functor $\Delta(N)$ in ${\bf C}^{\bf D}$, namely the constant functor $\Delta(N)$, which itself returns $N$ on any object. A limit is a terminal morphism from $\Delta$ to $F$, which means that it's a pair $\langle L,\phi\rangle$, with $L$ an object in ${\bf C}$ and $\phi:\Delta(L)\to F$ a natural transformation, so that any other natural transformation $\psi:\Delta(N)\to F$ factors as $\psi=\phi\circ u$, with $u:\Delta(N)\to\Delta(L)$ some other natural Transformation (as a not so relevant remark, $u$ is the arrow image of $\Delta$ for some arrow in ${\bf C}$). Now $\Delta(N)(X):=N$ for all $X$, i.e. the images of the constant functors comprise only one object. Therefore the arrow $u$ is determined by a single component $u_N$ from $N$ to $L$ and similarly, $\psi$'s components $\psi_X$ are all of type $N\to F(X)$. The fact that the domains of the components are always the same makes this definition equivalent with that in terms of the cone concept below - a cone is made up from the same data as a natural transformation where all components have the same domain.
Alternative definitions
Using cones
Our category of interest is ${\bf C}$. The category ${\bf D}$ is auxiliary and specifies some concept. The functor $F:{\bf C}^{\bf D}$ is used to specify that concept within out category of interest ${\bf C}$.
A cone is an object $N:\mathrm{Ob}_{\bf C}$ together with a ${\bf D}$-indexed family of arrows $\psi_X:N\to F(X)$ and such that every diagram which arises commutes. I.e. with it's “$\psi$-binocular”, the “tip of the cone” $N$ looks down on the whole image of $F$.
Finally, a limit is a cone given by $L,\phi$, which is as close at the image of $F$ as possible, in the sense that for all “higher” cones $N,\phi$, there is a unique arrow $u$ from $N$ to $L$ so that you can use the limit cone in favor of the other ones.
In the more abstract definition using the functor category, these several morphisms are encoded into a natural transformation (=a single morphism, but in another category). The trick is that a natural transformation is an arrow in a functor category and this way one can specify the limit as terminal morphism.
Discussion
The object of the limit is like the full solution to a problem posed by the concept captured by the functor.
Examples
Several example are linked with this entry.
An inverse limit is the special case of a limit where $J$ is essnetially an ordered grid (check for formals) and many important limits are even inverse limits. An interesting infinite example is the construction of the p-adic fields, see this SE thread.
Related
Three predicates relating to limits being carries to another category: A functor $G:{\bf C}\longrightarrow{\bf C}'$ takes a cone $\langle N,\psi\rangle$ in ${\bf C}$ to a cone in ${\bf C}'$. If the first is a limit and then the second one as well, then we say that $G$ preserves the limit. To define a cone, we needed a functor $F:{\bf D}\longrightarrow{\bf C}$. If $G$ preserves all limits for functors in ${\bf D}\longrightarrow{\bf C}$, then we say $G$ preserves all limits of type ${\bf D}$. If $G$ preserves all limits coming from a small category ${\bf D}$ (i.e. ${\bf D}:\mathrm{Ob}_{\bf Cat}$), then we say $G$ is a continuous functor.
Reference
Wikipedia: Limit (category theory)