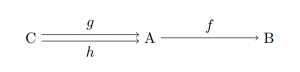Monomorphism
Collection
| context | ${\bf C}$ … category |
| definiendum | $f \in\mathrm{it} $ |
| inclusion | $f:{\bf C}[A,B]$ |
| postulate | $\langle A,\prod_{A}1_A\rangle$ … pullback of $f$ along itself |
Equivalent definitions
The arrow $f:{\bf C}[A,B]$ is mono of for all $g,h:{\bf C}[C,A]$ holds
$f\circ g=f\circ h\implies g=h$.
In ${\bf{Set}}$, this can be rewritten as the definition of injections:
$f(x)=g(y)\implies x=y$.
Theorems
The pullback of a mono is mono.
Discussion
The categorical definition above can easily be understood by considering ${\bf{Set}}$, where the pullback $A\times_BA$ is the set of pairs $\langle a,d\rangle\in A\times A$ for which $f(a)=f(d)$.
Say $f$ is not an injection and hence collapses two different terms $a,d\in A$ into a single value, i.e. $f(a)=f(d)$. The pullback object then contains $\langle a,a\rangle$ and $\langle d,d\rangle$, but also $\langle a,d\rangle$ and $\langle d,a\rangle$. So $A\times_BA$ is bigger than $A$. On the other hand, if $f$ is an injection, then for any $a$, the pullback only contains $\langle a,a\rangle$. We get $A\times_BA\cong A$.
The definition “$\langle A,\prod_{A}1_A\rangle$ is a pullback of $f$ along itself” implies that $A$ is already a valid pullback object, because $f$ doesn't collapse any information. Dually, the definition of an epimorphism (surjections in ${\bf{Set}}$) implies that $A$ is a valid pushout $A+_BA$, an object which generally contains less information than $A$.
A stepwise characterization of a monomorphism from the pullback, with a focus on the universal property, is given in pullback.