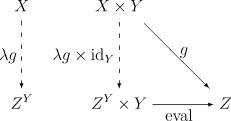This is an old revision of the document!
Terminal morphism
Collection
| context | $Z:\mathrm{Ob}_{\bf C}$ |
| context | $F$ in ${\bf D}\longrightarrow{\bf C}$ |
| definiendum | $\langle B,\phi\rangle$ in $\mathrm{it}$ |
| inclusion | $A:\mathrm{Ob}_{\bf D}$ |
| inclusion | $\phi:{\bf C}[FB,Z]$ |
| for all | $B:\mathrm{Ob}_{\bf D}$ |
| for all | $\psi:{\bf C}[FA,Z]$ |
| range | $f:{\bf D}[A,B]$ |
| postulate | $\exists!f.\ \psi=\phi\circ F(f)$ |
Discussion
Note that the name “terminal morphisms” for $\langle B,\phi\rangle$ is slightly confusing, because the data is not just the morphism $\phi$ going from $F(B)$ to $Z$, but also the object $B$.
Terminal and initial morphisms (the opposite notion, where you just flip some arrows) are called universal morphisms. They are a very important concept with a ridiculously broad range of examples, because you can essentially translate all “forall-there exists such that” characterizations to a “there is a universal morphism such that” characterizations. Another remark: Under a certain condition (namely that the construction works for all objects of a cateogry), the universal morphism gives an adjoint functor pair and indeed all adjoint functor pairs can be seen to arise that way.
In the following I'm going to elaborate what's going on a bit:
The main category you work in is ${\bf C}$. You fix an object $Z:\mathrm{Ob}_{\bf C}$ and what you want to do is to specify a special object and morphism with respect to it. Examples:
- You are given an object $Z$, which stores the information about two objects $X$ and $Y$. You want to characterize the product $X\times Y$ and the associated projection maps $\pi_1$ and $\pi_2$. With sets, that's the Cartesian product, but it also works with groups, respecting concatenation, or with topological spaces, this automatically introduces the product topology.
- Say you already know what products $\times$ for your category are. Given an object $Z$, you want to characterize exponential objects $Z^Y$ and evaluation map $\mathrm{eval}:Z^Y\times Y\to Z$. For example, in the category of sets, if $Y$ and $Z$ are objects, then the hom-set from $Y$ to $Z$ is of course the function space $Y\to Z$, and $Z^Y$ is exactly that space as object of ${\bf Set}$.
What the above definition says is the following: First you want to specify a smaller world within ${\bf C}$. You do this by setting up another category ${\bf D}$ and mapping it into ${\bf C}$ with a functor $F$. The image of $F$ is your smaller world. The universal morphism $\phi$ is then defined by demanding that every arrow from this small world, which tries to connect with the object $Z$, must pass through $\phi$. In other words (and now comes the definition): For all objects $B$ in ${\bf D}$, if $\psi$ is an arrow in ${\bf C}$ from $FB$ to $Z$, then there must be an arrow $f$ within ${\bf D}$, so that $\phi$ is really just a combination of “small world business” $F(f)$, followed by the kind of gate function $\phi$, finally leading to $Z$. For the reason that everything going on in the image of $F$ must pass to $Z$ only through $\phi$, one says $\phi$ is the terminal morphism “from the functor $F$ to the object $Z$”.
Example: The exponential object and currying
So you have a function $\psi:X\times Y\to Z$ and you want to be able to do partial function application, i.e. make sense of just passing an argument of $X$ to $\psi$ and leave the second component unevaluated. In plain English, we need the function space which contains the half-evaluated function. To make use of it, we also need the evaluation function, which when passed the half-evaluated function and an argument of $Y$ returns the same as what $\psi$ would do.
It's done as follows: We have $Z:\mathrm{Ob}_{\bf C}$. Now fix any “second argument space” $Y$. Define the object map of the auto-functor $F$ as $FA:=A\times Y$ and its function map by $F(f):=f\times\mathrm{id}_Y$. Now we are done by asking for the terminal morphism from $F$ to $Z$: This exactly means the category must contain a function object, let's call it $Z^Y$, so that for any $\psi:X\times Y\to Z$ (which is $\psi:FX\to Z$) there is a function $f$, which chooses a function $F(f)(x)$ in $Z^Y$, so that $\psi$ can be written as first passing $\langle x,y\rangle:X\times Y$ to $\langle F(g)(x),y\rangle$ and then evaluates this via $\mathrm{eval}(F(f)(x),y):=\left(F(f)(x)\right)(y)$.
(The left side is in ${\bf D}$, the right is in ${\bf C}$ and $f$ is called $\lambda g$ here.)
As a side note: As this works for all $Z$, this gives rise to a hom-class adjunction of the above functor $F$ and the one mapping $Y$ to $Z^Y$. The categorical currying is hence $\mathrm{hom}(X\times Y,Z)$ being isomorphic to $\mathrm{hom}(X,Z^Y)$. The nice thing is, of course, that this doesn't just work for categories with function, but the same construction also works when reasoning about logic, where currying then is the tautology $\left((A\land B)\implies C\right)\Leftrightarrow \left(A\implies(B\implies C)\right)$.
Adjoint functors
To state the definition again, with a little different notation: A terminal morphism from $F$ to $X$ is a pair $\langle O_X,\varepsilon_X\rangle$, where $\varepsilon_X:FO_X\to X$, such that for any $f:FY\to X$, there is a morphism $g_f:Y\to O_X$ in the other category, so that $f$ factors as $f=\varepsilon_X\circ F(g_f)$.
Now if that construction happens to work for all $X$, then it gives rise for the dual initial morphism construction in the other category as follows: By assumption now, for all $X$, there is a universal morphism $\langle O_X,\varepsilon_X\rangle$ from $F$ to $X$. In particular, the factoring works for the identity morphism at $FY$, i.e. $\mathrm{id}_{FY}=\varepsilon_Y\circ F(g_{\mathrm{id}_{FY}})$ with $g_{\mathrm{id}_{FY}}:FY\to O_{FY}$. We denote the so constructed morphism by $\eta_Y:=f_{\mathrm{id}_{FY}}$ and it's the pendant of $\varepsilon_X$ in the other category. We can now introduce a functor $G$ by setting the object map $GX:=O_X$ and the arrow map such that the following diagram commutes
Even more, we find $\varepsilon:\mathrm{nat}(FG,1_{\bf C})$ and $\eta:\mathrm{nat}(1_{\bf D},GF)$. Therefore, all of this is equivalent to the gadgetry defined in counit-unit adjunction.
Reference
Wikipedia: Universal property, Exponential object