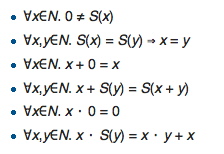Univalence axiom
Note
Axiom:
| $Id_U(A,B)\simeq(A\simeq B)$ … is inhabited |
Discussion
LHS: Here $A,B:U$ are some types in a universe. The identity type $Id_U(A,B)$ corresponds (in the groupoid pov) to the space of paths from $A$ to $B$ in $U$.
RHS: Here the type equivalence $(A\simeq B)$ is defined in terms of functions running in opposite directions, $A\to B$ and $B\to A$.
Per definition, the identity type $Id_U(A,A)$ is inhabited by the term $refl_A$ and this corresponds to the (invertible) identity function $id_A:A\to A$. Now more generally, adding the univalence axiom gives means to the identity type of the theory by “filling it up” with functions from the type of equivalences. In other words, what's relevant is the corrolary “there is a function of type $(A\simeq B)\to Id_U(A,B)$”.
In the following we outline why this is a good idea, if we want to use our type theory to formulate mathematics.
Motivation
Theories and their equalities
In equalitarian propositional logic, equality between two terms is a relation which per default is taken to be reflexive, symmetric and transitive. We can set up theories in logic (of numbers, of set elements, of group elements,…) and then further specify how to work with it via axioms.
Examples
On the right hand side we have the rules for equality for Peano arithmetic (PA), which is a theory of natural numbers in terms of symbols $0, S$ and $+$. Using those we can prove $SS0+SSS0=_{PA}SSSSS0$, which, after making the definitions $1\equiv S0,\,2\equiv S1,\,etc.$ translates to $2+3=_{PA}5$. Meanwhile, the “axiom of extensionality” $\forall x.\,\forall y.\left(\forall z.\,(z \in x \Leftrightarrow z \in y) \Rightarrow x = y\right)$ is an axiom of Zermelo-Freankel set theory (ZF), which are theory of sets in terms of symbols $\in$. Using those we can prove $\{x,x,y\}=_{ZF}\{x,y\}$.
Set theoretical models
In set theory, we can make models of other structures so that truths of their theories are reflected as truths of sets. For example, one commonly defines ${\bar 0}\equiv\{\}$, ${\bar S}x\equiv x\cup\{x\}$ and addition ${\bar +}$ in such a way that ${\bar S}{\bar S}{\bar 0}{\bar +}{\bar S}{\bar S}{\bar S}{\bar 0}=_{ZF}{\bar S}{\bar S}{\bar S}{\bar S}{\bar S}{\bar 0}$ can be proven. All those sets (representing numbers) are then collected and put into a set $\mathbb N_{ZF}\equiv\{{\bar 0},{\bar S}{\bar 0},{\bar S}{\bar S}{\bar 0},\dots\}$
Another example is the model of the ordered pair $\langle x,y\rangle\equiv \{\{x\},\{x,y\}\}$ and then the following desired statement can be proven: $(\langle x,y\rangle=_{ZF}\langle u,v\rangle)\Leftrightarrow (x=_{ZF}u\land y=_{ZF}v)$. Furthermore, a group can be modeled as a pair $\langle G,*\rangle$, where $G$ is a set of group elements and $*$ is the function defining the multiplication table. Then the group $\mathbb Z_2$ of two elements can be presented as ${\mathrm z}_2^+\equiv\langle\{0,1\},+\rangle$ or ${\mathrm z}_2^\times\equiv\langle\{1,-1\},\times\rangle$, where $+$ is arithmetic addition mod $2$ and $\times$ is arithmetic multiplication.
Because of its capacity to define models set theory can be taken as foundation for mathematics. One only needs <logic and set theory axioms and definition of concepts in terms of sets> as opposed to <logic and new axioms for each theory>. The backside of this approach that both $=_{ZF}$ and $\in$ inherit unwanted truths. For exmaple:
- Using the definition above, we can prove $1\in\langle 0,5\rangle$ and similarly $\{2\}\in {\mathrm z}_2^+$.
- As far as their group structural properties go, ${\mathrm z}_2^+$ and ${\mathrm z}_2^\times$ are the same, but it's also clear that we can prove ${\mathrm z}_2^+\neq_{ZF}{\mathrm z}_2^\times$.
If you write down mathematics in type theory, it's not that you start with objects and group them together to a collection (like with sets). So there is no equivalent of odd statements like $\{\}\in\mathbb N_{ZF}$. Theat last statement is true in the above set theoretic implementation (model) for the natural numbers, btw., but will be false in many other models of them.
Category theory
Another theory which is mostly use to discuss other theories is category theory. It itself is written down in logic or type theory or modeled within set theory.
On the level that category theory is investigating mathematical structures (e.g. when dealing with the category of rings, as opposed to individual ring elements) one often doesn't need or want an equality $=_{Category}$, because the structures come with a refined notion of sameness (e.g. ring isomorphisms). Indeed, category theoretical properties are purposely always formulated only up to isomorphism (=universal properties). An arrow is called isomorphism, if there is another arrow pointing in the opposite direction, such that their composition is the identity (and if we deal with higher categories, then this also need to hold only up to isomorphism). But the details to when two arrows are inverses (up to isomorphism) depends on the category under consideration. For example, we can define the category of rings where arrows are ring homomorphisms and then the number of ring isomorphisms vary depending on which two objects we consider.
Homotopy type theory
Martin-Löf type theory contains a notion of identity $Id_A$, which has computational content (complicated rules of substitution, see nLab: Identity type) and also gives rise to an $\infty$-groupoid structure, see identity type. The theory comprises a programming language. This should be viewed in contrast with equalitarian propositional logic, where proof theory is done on a meta-level. However, being dependent on the type $A$, the identity type $Id_A$ is still closer to the general logical equality than to the set theoretical equality $=_{ZF}$ fixed right away is fixed by a bunch of set theory axioms.
With the univalence axiom, homotopy type theory extends on Martin-Löf type theory by adopting a structural perspective on equality.
$Id_U(A,B)\simeq(A\simeq B)$
Here $\simeq$ is defined like a homotopy equivalence, in support of the $\infty$-groupoid pov. (I've written down some explanations of the univalence axiom in the HoTT Wikipedia article.)
An isomorphism of a plain set is of course an invertible function - a bijection. Note that if by the set of natural numbers and set of rational numbers you merely mean the collection of their elements, then they are equal in HoTT (there is a bijection)! But as soon as you consider them equipped them with their structure (e.g. $+$ arithmetic), they are not equal.
On a slightly more technical note
In Martin-Löfs type theory, having a term of the identity type $Id_U(A,B)$ allows for substitution between the expression $A$ and $B$. Knowing this, going from the LHS to RHS in the axiom is actually “trivial”. Having a term $p$ of $Id_U(A,B)$ lets you change the identity function $id:A\to A$ at $A$ into a function $id^p:A\to B$, which is “invertible” and so you found a term of $A\simeq B$. The univalence axiom can be formulated as saying that this procedure always also works in the other direction from RHS to LHS, so that it's actually an equivalence.
Sets in HoTT
The notion of set in HoTT reflects that of a strict discrete category, where there are no non-trivial arrows. A set here is merely a collection of things devoid of structure.
$isSet(A):={\large\Pi}_{x,y:A}\,isProp(Id_A(x,y))$
“The type $A$ is a set if all it's terms are equal in at most one way”
Name
If we take the type theory as starting point, the name “univalent” is a technical nomenclature in its categorical semantics.
Some confusing notes I want to take before I understand this further: You have the diagonal map “$\Delta_A:A\to(A\times A)::a\mapsto\langle a,a\rangle$”. The image of $\Delta_A$ represents the equality relation. Now if $p:A^I$ is a path in $A$ and if $ends(p):=\langle p_0,p_1\rangle$ maps it to its endpoints, then any map $aloop:A\to A^I$ which maps $A$ to some loop provides a factorization of $\delta=ends\circ aloop$. Now, roughly, if $end$ is invertible, we can replace the substitute relation with the path object.
What's not mentioned in this comments is that all of this must be done for types $a:A\vdash Q(a):\mathrm{Type}$. Only then, i.e. if there is more structure going on, can the above “inversion” be nontrivial.
see nLab: univalence axiom
Reference
nLab: Identity type, univalence axiom