Yoneda embedding
Functor
| context | ${\bf C}$ … small category |
| definiendum | $\mathcal y$ |
| inclusion | $\mathcal y$ in ${\bf C}\longrightarrow{\bf Set}^{{\bf C}^\mathrm{op}}$ |
| definition | $\mathcal y\,A:=\mathrm{Hom}_{\bf C}(-,A)$ |
| definition | $\mathcal y(\,f):=g\mapsto f\circ g$ |
Discussion
Elaboration on the action on arrows
Consider a general arrow $f:{\bf C}[A,B]$.
In the presheaf category ${\bf Set}^{{\bf C}^\mathrm{op}}$, the image arrow
$\mathcal y(\,f)$ in $\mathrm{nat}\left(\mathrm{Hom}_{\bf C}(-,A),\mathrm{Hom}_{\bf C}(-,B)\right)$
is the natural transformation, with components
$y(\,f)_X:{\bf C}[X,A]\to{\bf C}[X,B],$
mapping an arrow $g$ to an arrow $f\circ g$. So by post-composition, this just redirects arrows in ${\bf C}[X,A]$ to arrows in ${\bf C}[X,B]$.
Nationality of the fmap
Let $g: X\to Y$ and $f: A\to B$.
We make $f$ into a natural transformation from $\mathrm{Hom}(-,A)$ to $\mathrm{Hom}(-B)$ via the following square:
$h: \mathrm{Hom}(Y,A)$ … $f\circ h : \mathrm{Hom}(Y,B)$
$h\circ g : \mathrm{Hom}(X,A)$ … $f\circ h\circ g : \mathrm{Hom}(X,B)$
Note how the $\mathrm{Hom}$-functors themselves are contravariant, as seen by the direction of the vertical arrows: $g: X\to Y$ but e.g. the associated fmap goes from $\mathrm{Hom}(Y,A)$ to $\mathrm{Hom}(X,A)$.
Yoneda lemma
The Yoneda lemma says that this functor $y$ is full and faithful, implying there are no other natural transformations between the hom-functors than the ones arising from arrows in $\bf C$. For the following elaborations, recall two things:
- Consider a small category ${\bf C}$ and a category ${\bf D}$. In the functor category ${\bf D}^{\bf C}$, the objects are functors $F,G,H,\dots$ and arrows are the natural transformations.
- Consider a small category $\bf C$ and any $A:\mathrm{Ob}_{\bf C}$. We have the map $\mathrm{Hom}_{\bf C}(-,A)$, which sends objects $X$ to the hom-set ${\bf C}[X,A]$. Let's emphasize that $\mathrm{Hom}_{\bf C}(-,A)$ is the contravariant set-valued functor, which knows about all functions into $A$. For example if $A=\mathbb R^2$, then the image of $\mathbb S^1$ under $\mathrm{Hom}_{\bf C}(-,\mathbb R^2)$ is the space ${\bf C}[\mathbb S^1,\mathbb R^2]$ of embeddings of the circle into the plane.
Special case for Hom - Yoneda embedding
As a warm-up, Consider a singleton $1$ in $\bf Set$ and notice that ${\bf Set}[1,A]$ is in bijection with $A$ itself. So if $A,B,\dots$ are the objects of $\bf Set$, then I can provide you with ${\bf Set}[1,A],{\bf Set}[1,B],\dots$, and just by adding all possible functions between them, you can fully reconstruct $\bf Set$. If ${\bf Set}[1,A]$ already knows everything about $A$, then so does the functor $\mathrm{Hom}_{\bf Set}(-,A)$, which lives in a functor category.
Now we consider a category ${\bf C}$, let's write $h_A:=\mathrm{Hom}_{\bf C}(-,A)$ and think of $h_A$ as objects in the functor category ${\bf Set}^{{\bf C}^\mathrm{op}}$. How do the arrows between objects $h_A,h_B$ etc., i.e. the natural transformations, relate to the arrows between the initial objects $A,B$? The special case of the Yoneda lemma for the Hom-functor, says that they are in fact already (naturally) isomorphic! For all $A,B\in {\bf C}$, we have:
| ${\bf Set}^{{\bf C}^\mathrm{op}}[h_A,h_B]:=\mathrm{nat}(h_A,h_B)\cong{\bf C}[A,B]$ |
|---|
The cool thing of the lemma is that it says you can super-size the objects by passing from objects $A$ of $\bf C$ to objects $h_A=\mathrm{Hom}_{\bf C}(-,A)$ of ${\bf Set}^{{\bf C}^\mathrm{op}}$, but then the arrow structure there isn't new. Morally, the objects are replaced by the totality of ways of looking a them: “A thing is only the sum of its relations to the rest of the world”.
The nice thing also is that the ambient category will contain new objects (functors) that relate to the original category. In particular, the functor category is the “free co-completion”: disjoint sum-like objects are guaranteed to exist, etc., just as for sets. See also the discussion in Set.
General version
Consider a (locally Cartesian closed, I think) category $\bf C$. The Yoneda lemma now says that the above construction works for any contravariant functor $F$ which represents your mathematical structure in terms of sets (presheaf):
| ${\bf Set}^{{\bf C}^\mathrm{op}}[h_A,F]:=\mathrm{nat}(h_A,F)\cong F\,A$ |
|---|
This might be read in two directions:
- Left to right: The arrow structure in the functor category isn't more complicated than the object-images of the functors in it - thank god! (The arrows there are so restricted because per definition they are natural transformation and those respect the initial Hom-structure in $\bf C$.)
- Right to left: For set-value functors $F$, their image is isomorphic to the possible representations of $F$ by the Hom-functors.
The Hom-functors, which know about this arrow structure, are the most important objects in the functor category.
Important remark: And the Yoneda lemma works just as much for covariant functors $G$ and then involves $h^A:=\mathrm{Hom}_{\bf C}(A,-)$.
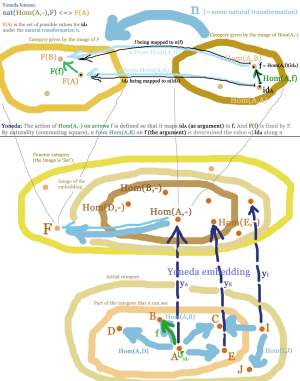
The following picture is taken from Tom Leinsters “The Yoneda Lemma - What is it all about”:
Here is an image, which “explains” the Yoneda lemma and its proof:
Reference
Wikipedia: Yoneda lemma,
nLab: Yoneda lemma, Yoneda embedding