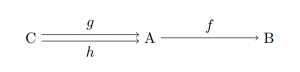Pullback . category theory
Collection
| context | $F:({a\rightarrow z\leftarrow b})\longrightarrow{\bf C}$ |
| definition | $\langle Fa\times_{Fz} Fb, \pi\rangle := \mathrm{lim}\,F$ |
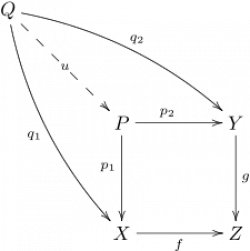
Here we consider a functor $F$ from the category ${a\rightarrow z\leftarrow b}$, consisting of three object and two non-identity arrows $f_a$ and $f_b$, to a category ${\bf C}$.
Universal property
For readability, let's write $A\equiv{Fa}, B\equiv{Fb}, Z\equiv{Fz}, \alpha\equiv{f_a}$ and $\beta\equiv{f_b}$.
(In the picture we have $X\equiv{Fa}, Y\equiv{Fb}, Z\equiv{Fz}, f\equiv{f_a}, g\equiv{f_b}$ and the pullback object is $P\equiv X\times_Z Y$.)
Consider two arrows $\gamma:{\bf C}[X,A]$ and $\delta:{\bf C}[X,B]$, which fulfill the structural condition $\alpha\circ\gamma=\beta\circ\delta$. I.e. when forwarded to $Z$ via $\alpha$, resp. $\beta$, they collapse into a single arrow.
Such two arrows $\gamma,\delta$ can be partially glued together, in the sense that they can both be written as a unique arrow $u$ (with codomain $A\times_Z B$) followed by the projections $\pi_a,\pi_b$.
Discussion
The pullback object $A\times_Z B$ is the full solution to the equation posed by $\alpha$ and $\beta$. In ${\bf{Set}}$, it's literally the set of pairs $\langle x,y\rangle\in A\times_Z B\subseteq A\times B$, for which $\alpha(x)=\beta(y)$.
When the category contains a terminal object $1$ (where $\alpha$ and $\beta$ are trivial arrows and form a trivial condition), we have $A\times_1 B\cong A\times B$.
The universal property says that all other solution embed in this object, in this is what is meant by full solution.
Special cases
- If $\pi_a$ is an iso, then $A\times_Z B\cong A$. As $A$ is already the pullback, it alone fully determines the “full solution”.
- If moreover $\pi_b$ is an iso too, the projections, we can consider the equivalent pullback with $\pi_b=\pi_a=1_A$. The universal property now says that arrows $\gamma,\delta$ can be wholly glued together: Up to iso, $\alpha\circ\gamma=\beta\circ\delta\implies\gamma=\delta$.
- In ${\bf{Set}}$, if $\alpha=\beta$, the pullback definition says that its elements $\langle x,y\rangle$ fulfill $\alpha(x)=\alpha(y)$, i.e. here the pullback object is the full collection of pairs of term with give the same $\alpha$ value. If moreover $\pi_a$ is iso, any $x$ determines an $\langle x,y\rangle$ and hence an $y$ and the universal property translates to $\alpha(x)=\alpha(y)\implies x=y$. This is just the definition of an injection.
- Back to a general category. If the pullback of $\alpha$ along itself ($\alpha=\beta$) is such that a projection $\pi_a$ is iso, we call $\alpha$ a monomorphism. The associated condition reads $\alpha\circ\gamma=\alpha\circ\delta\implies\gamma=\delta$.
(In the picture, $f$ is $\alpha$ and $g,f$ are our $\gamma, \delta$.)
Examples
A finite pullback in ${\bf{Set}}$ that I just made up:
- Generally: If $F(f_b)$ is the inclusion of a subset $Fb\subseteq{Fz}$ in ${Fz}$, the pullback is iso to (i.e. in bijection with) $F(f_a^{-1})Fb$. Further, if $F(f_a)$ is an inclusion too, this is in bijection with $Fa\cap{Fb}$. If the subset-interpretation doesn't apply, the function $F(f_b)$ from $Fb$ to $Fz$ should be viewed as defining fibre bundle over $Fz$ and the pullback gives a fibre bundle from $Fa\times_{Fz} Fb$ to $Fa$.
- A concrete example: Let
$Fa=\{2,4,6,8\},\ Fb=\{10,20\},\ Fz=\{77,88,99\}$
$F(f_a)(2)=77,\ F(f_a)(4)=77,\ F(f_a)(6)=88,\ F(f_a)(8)=99$
$F(f_b)(10)=88,\ F(f_b)(20)=77$
Then
$Fa\times_{Fz} Fb=\{\langle 2,20\rangle,\langle 4,20\rangle,\langle 6,10\rangle\}$
and $\pi$ are projections like for the product.
Two more prominent examples:
- If $M$ is a manifold, $p:B\to M$ is a fibre bundle over $M$ and $f:X\to Y$ is an embedding of another manifold $X$ into $Y$, the the pullback object is a fibre bundle over $X$, namely the differential geometric pullback.
- In $\bf{Set}$, if the “central object” is $\Omega=\{0,1\}$, the right function comes from a singleton $1$ and if the left function $\chi:X\to \Omega$ is a characteristic function, then a pullback object is a subset of $X$: It's defined as collection of arguments where the characteristic function agrees that the value is $1$. This works also for more general “fuzzy” $\Omega$. These $\Omega$ are the “objects of truth values” and are called subobject classifiers.
Digression: The exponential object $B^A$ is a prominent example of an object which isn't a limit, but it can be specifies via universal morphism construction. For sets or types, that's the function space $A\to B$ and for propositions it's the implication. If a category has product, exponential object and a terminal object, then it's called Cartesian closed. A Cartesian closed category with subobject classifier is a topos. We see now how a topos is a general kind of set theory, and simultaneously defines an internal logic.
Reference
Wikipedia: Pullback (category theory), Subobject classifier