Hask
Note
todo:
objects are types
arrows are extensionally identified Haskell functions
identity morphism: for each object, the identity morphism is the instance of the polymorphic identity for that type
The identity for a type 'a' is '(id :: a→a)' and concatenation is 'f . g', defined as '\x → f (g x)'.
Discussion
Hask is the syntactic subset of Haskell which permits a whole bunch of operations that are seen in basic category theory.
With $\to$ and $\times$ etc., Hask is almost Cartesian closed. A particular problem is the polymorphic term 'undefined', which is defined to be term of every type. It prevents, for example, initial objects (i.e. there no analog to the “empty set”). Or when it comes to setting up the categorical product, the projections $\pi_1,\pi_2$ couldn't distinguish between $'(\text{undefined},\text{undefined})'$ and just $\text{undefined}$, spoiling uniqueness. See Hask for more examples.
As far as some basic category theoretical concepts go, Hask is the largest collection of types in Haskell but by more restriction, you can find some actual and nicely behaved categories. See also the category-extras package.
Another deficit is that when it comes to passing functions as arguments, Haskell sees more than just Hask morphisms. A nicer definition of the largest category of Haskell would be if arrows weren't Haskell functions identified by function extensionally ($\forall x. f(x)=g(x)\implies f=g$), but rather identified if equivalent when passed to other Haskell functions as arguments ($\forall h. h(f)=h(g)\implies f=g$, see indiscernibility of identicals. We can back the first definition if we consider only the eval-functions for $h$'s).
However, this doesn't work: With the definition of concatenation given above, the category laws imply that '(undefined :: Int → Char).id' must be '\x →(undefined :: Int → Char) x'. But there are functions which can detect the non-extensive property of 'undefined :: Int → Char' being the 'undefined' term for the type 'Int → Char'. The function 'seq' (which is implemented to make enforcement of strict evaluation possible) will return a different result when passed the extensionally equal functions 'undefined :: Int → Char' and '\x →(undefined :: Int → Char) x'.
Functors
In the following I present some images elaborating on the connection between Haskell-features to category theory, just click the images to display a larger version.
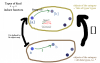
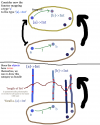
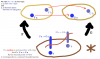
Functors and fmap:
Polymorphism / Fibre bundles:
Natural transformations:
this has the right type. todo: check defining property of Natural transformation.
The $\text{flatten}$ example given in this blog in the section “2.2. Meaning of polymorphism” is a non-academic example.
Monads:
These are explained in the entry Hom-set adjunction.
Discussion
Reference
haskell.org: Hask, category-extras
Wikibooks: Category theory for and in Haskell