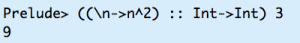Haskell type system
Note
Haskell has a two-level type system. There kinds which are inhibited by types, and these types are further inhibited by terms. Kind and type inference can be done in the Haskell ghci-environment via ':k' and ':t', respectively.
Kinds
The syntax for kinds is pretty simple. The most relevant kind to discuss is $\star$, the kind of data types. There is furthermore an important 2-ary symbol $k_1\longrightarrow k_2$. If $k_1,k_2$ are kinds of finite depth, then $k_1\longrightarrow k_2$ is a kind with inhabitants called type constructors.
Examples for kinds and their inhibiting types
$\mathrm{Int}\ :\ \star\hspace{1cm}$ … type of integers
$[]\ :\ \star\longrightarrow\star\hspace{1cm}$ … list type constructor
$[\mathrm{Int}]\ :\ \star\hspace{1cm}$ … type of lists of integers
$(\to)\ \mathrm{Int}\ :\ \star\longrightarrow\star\hspace{1cm}$ … functions from integers type constructor
$(\to)\ \mathrm{Int}\ \mathrm{Int}\ :\ \star\hspace{1cm}$ … type of functions from integers to integers, which is also written in infix notation, $\mathrm{Int}\to\mathrm{Int}$
$(\to)\ :\ \star\longrightarrow\star\longrightarrow\star$
Next to $\star$, another relevant 0-ary kind is $\mathrm{Constrained}$. We'll come back to it in the section on type classes.
Data Types
Haskell has some in-build data types ($\mathrm{Int}$, $\mathrm{Bool}$, …), see Prelude. Some possibilities to create new ones is discussed in the following.
To keep things simple, the following examples don't employ type polymorphism. Hence, all type variables $a,b$ should be thought of as replaced by concrete types.
Function types
Type theoretically (on the kind level): ${\large\frac{a\ :\ \star \hspace{.5cm} b\ :\ \star}{a\to b\ :\ \star}}$
Haskell syntax:
a->b
Type theoretically: ${\large\frac{x\ :\ a \hspace{.5cm} g\ :\ b}{\lambda x.g\ :\ a\to b}}$
((\x->g) :: a->b)
for example
((\n->n^2) :: Int->Int) 3
Due to Haskells type inference, the annotation “::a→b” is often optional.
And there are many in-build functions such as the logical 'and' or the arithmetic '+'.
Product types
There is the product type $a\times b$ (Cartesian product/direct product/logical and), written
(a,b)
But notice that there is automatical currying and so it doesn't appear in function declaration as often as one might guess. Here an example with only one type $a$. Let's write $\mathrm{TripleType}(a)\equiv a\times a\times a$. Then
${\large\frac{a\ :\ \star}{\mathrm{TripleType}(a)\ :\ \star}}$,
${\large\frac{x,y,z\ :\ a}{\langle x,y,z\rangle\ :\ \mathrm{TripleType}(a)}}$
Haskell syntax is
type TripleType a = (a,a,a)
Now we can ask ':k TripleType' and ':k TripleType Int' and find $\star\longrightarrow\star$ and $\star$, respectively.
Algebraic data types
Algebraic data types are a more free means to create types. In general one specifies a kind of type sum (disjoint union/direct sum/logical or) of one or more alter- natives, where each alternative is a product of zero or more slots. Uppercase words for are used for constructions, for example, there is $\mathrm{Either}$.
The standard example is this: Let $a$ be a type variable. Say we want to make a type of binary tree graphs for $a$, where a term is either a term of $a$ or forking branch. In type theoretic notation:
${\large\frac{a\ :\ \star}{\mathrm{Tree}(a)\ :\ \star}}$
${\large\frac{x\ :\ a}{\mathrm{Leaf}(x)\ :\ \mathrm{Tree}(a)}}$, ${\large\frac{s,t\ :\ \mathrm{Tree}(a)}{\mathrm{Branch}(s,t)\ :\ \mathrm{Tree}(a)}}$
data Tree a = Leaf a | Branch (Tree a) (Tree a)
The introduced key words $\mathrm{Leaf}$ and $\mathrm{Branch}$ are further used for pattern maching. E.g. in the function definition
size :: Tree a -> Int size (Leaf x) = 1 size (Branch t u) = size t + size u + 1
Polymorphic types
Haskell also supports types with $\forall$-quantified type variables, e.g. $\forall a.a\to a$, like System F. An example for a defintion for a terms polymorphic type is
map :: forall a b. (a -> b) -> [a] -> [b]
This type is parametrically polymorphic.
Type checking (and "Kind checking", if you will) examples in ghci
Type classes
We introduce the 'class' keyword. It lets us specify subsets of types or type constructors by demanding implementations of associated functions. Members of these subsets are then instantiated with the 'instance' keyword, where you write specific implementations of the function. This is called ad hoc polymorphism, the less nice polymorphism.
Example
The class $\mathrm{Integral}$ contains $\mathrm{Int}$ and $\mathrm{Integer}$. It is a subset of $\mathrm{Real}$, which also contains $\mathrm{Float}$ and $\mathrm{Double}$. Which in turn is a subset of $\mathrm{Eq}$, which contains many more types. For any two terms $x,y$ of a type in $\mathrm{Eq}$, the function application of $==$ makes sense. To quote the definition of the simple $\mathrm{Eq}$-class:
class Eq a where (==), (/=) :: a -> a -> Bool
While 'class' is a keyword, $\mathrm{Eq}$ is an operation with kind $\star\longrightarrow\mathrm{Constraint}$.
For $\mathrm{Eq}$ instance, it's worth pointing out that if you skip writing one of of the two function instances, Haskell will try
x /= y = not (x == y) x == y = not (x /= y)
Category theory
The kind $\star$ can be viewed as the objects of certain category, see Hask. The kind $\star\longrightarrow\star$ can be viewed as the object map of Hask-endofunctors. Indeed, functors are formalized in Haskell as the class of type constructors $\star\longrightarrow\star$ for which an associated function map 'fmap' is implemented.
class Functor f where fmap :: (a -> b) -> (f a -> f b)
(See Functor . Haskell)
The operation Functor is of kind $(\star\longrightarrow\star)\longrightarrow\mathrm{Constraint}$. Hence any instance $f$ will be of kind $\star\longrightarrow\star$.
There is no Haskell-mechanism which enforces laws on class members, so one should only instantiate a member of $\mathrm{Functor}$ if it does respect the identity and composition law.
Examples
This is the example of the fairly obvious $\text{fmap}$-implementation for the List-Functor (“List” has it's own name, namely “[]”):
instance Functor [] where fmap _ [] = [] fmap g (x:xs) = g x : fmap g xs
The type system derives which fmap to use from the fact that we apply the construction to a list.
The following example is the functor whose object map maps each type to a type, where each of the old terms have a clone with the prefix '$\text{Just}$', and there is more over an additional term called nothing '$\text{Nothing}$':
instance Functor Maybe where fmap _ Nothing = Nothing fmap g (Just a) = Just (g a)
This can be used to deal with exceptions.
For all types $a$, the constructor $(\to)\,a$ is the object map of $\mathrm{Hom}_\mathrm{Hask}(a,-)$.
In fact, all of the functors mentioned can be made into monads, and they are known as list, maybe and reader monad.
Reference
Wikipedia: Kind (type theory)