Presheaves can be understood as spaces in the following way:

Topoi can be viewed as universes of things. The archetypical topos is ${\bf{Set}}$ and all topoi have many of it's nice features, e.g. local Cartesian closure and existence of small (co-)limits. Any presheaf category ${\bf{Set}}^{\bf{C}^{op}}$ (objects=presheaves, arrows=natural transformations) is a topos. (Remark: and since ${\bf{Set}}\cong{\bf{Set}}^{\bf{1}}$, the category of sets is in fact an example of such a presheaf category).

The Yoneda embedding maps initial category ${\bf{C}}$ into a topos of presheaves: For any $U\in{\bf{C}}$, there is always the Hom-functor presheaf $\mathrm{Hom}_{\bf{C}}(-,U)\in{\bf{Set}}^{{\bf{C}}^{op}}$ and for any arrow $\beta:{\bf{C}}[U,W]$, there is always the natural transformation taking $\alpha\in\mathrm{Hom}_{\bf{C}}(V,U)$ to $\gamma\in\mathrm{Hom}_{\bf{C}}(V,W)$ via $\gamma:=\beta\circ\alpha$.

todo: draw commuting triangle
$V\overset{\alpha}{\mapsto}U\overset{\beta}{\mapsto}W=V\overset{\gamma}{\mapsto}W$

Therefore, the topos ${\bf{Set}}^{\bf{C}^{op}}$ contains a copy of ${\bf{C}}$.

Please also see the idea discussion in Functor category.

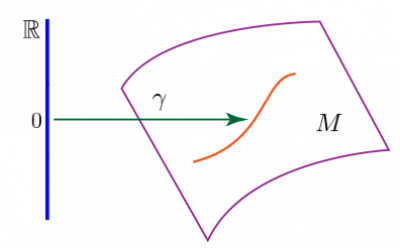
Geometric picture: If $\bf{C}$ is thought of as category of spaces, then the Yoneda embedding $U\mapsto\mathrm{Hom}_{\bf{C}}(-,U)$ maps the space $U$ to the ways of laying out other objects within $U$.

Example: If $\bf{C}=\bf{CartSp}$ is the category with objects

$\mathrm{Ob}_{\bf{CartSp}}=\{\{\emptyset\},{\mathbb R},{\mathbb R}^2,{\mathbb R}^3,{\mathbb R}^4,\dots\}$

and smooth functions (w.r.t. the standard topology) between them, then e.g.

$\mathrm{Hom}_{\bf{C}}(-,{\mathbb R}^3)\in{\bf{Set}}^{\bf{CartSp}^{op}}$

is the information of how to put points into ${\mathbb R}^3$, how to lay out smooth lines in ${\mathbb R}^3$, how to lay out smooth surfaces in ${\mathbb R}^3$, how to fold ${\mathbb R}^7$ within ${\mathbb R}^3$, and so on.

A general space $M$ from the theory of differential manifolds is of course not an object of $\bf{CartSp}$. Nevertheless, we know how to set up the presheaf $X\in{\bf{Set}}^{\bf{CartSp}}$, which maps any ${\mathbb R}^k\in{\bf{CartSp}}$ to the smooth maps from ${\mathbb R}^k$ to $M$, i.e. “$\mathrm{Hom}_{\bf{CartSp}}(-,M)$”. So we see how the topos $\bf{Set}^\bf{CartSp}$ is much richer than $\bf{CartSp}$. $\Box$

Geometric meaning of the Yoneda lemma: Consider again the objects $\mathrm{Hom}_{\bf{C}}(-,U)$ and $\mathrm{Hom}_{\bf{C}}(-,W)$ in ${\bf{Set}}^{\bf{C}^{op}}$, now with emphasis on viewing them as the ways to lay out any space $V$ within the spaces $U$ and $W$. We saw that if $\beta\in\mathrm{Hom}_{\bf{C}}(U,W)$ is a way of laying out $U$ in $W$ and if $V$ is another space, then we can use $\beta$ to redirect any $\alpha\in\mathrm{Hom}_{\bf{C}}(V,U)$ to a $\gamma\in\mathrm{Hom}_{\bf{C}}(V,W)$ via $\gamma:=\beta\circ\alpha$. In fact, all ways of redirection work this way $${\mathrm{nat}}(\mathrm{Hom}_{\bf{C}}(-,U),\mathrm{Hom}_{\bf{C}}(-,W))\cong \mathrm{Hom}_{\bf{C}}(U,W).$$ This says that the Yoneda embedding is faithful.

Note that the validity of this concept carries over to the above example. E.g. if you have a way $\beta$ to embed ${\mathbb R^2}$ as a surface in a 3-dimensional manifold, say, and further an embedding of a line $\alpha\in\mathrm{Hom}_{\bf{CartSp}}({\mathbb R},{\mathbb R^2})$, then $\gamma:=\beta\circ\alpha$ clearly smoothly maps ${\mathbb R}$ to $M$.

As noted, not all presheaves $X\in{\bf{Set}}^{\bf{C}^{op}}$ are representable, i.e. there might be no space $M$ living in $\bf{C}$ so that $X\cong\mathrm{Hom}_{\bf{C}}(-,M)$ and we might not even be able to set up a good category $\bf{C}$ where such an object $M$ exists. However (!), the point is that if you work within the topos ${\bf{Set}}^{\bf{C}^{op}}$ instead of $\bf{C}$, then this isn't even necessary, because as soon as you define a presheaf $X$ somehow, everything behaves as if there where a space $M$. The reason is the co-Yoneda lemma: $${\mathrm{nat}}(\mathrm{Hom}_{\bf{C}}(-,U),X)\cong XU.$$ This says that, while $\beta\in XU$ might not itself be a way to lay out $U$ in some actual space $M$, it nevertheless corresponds to a way of redirecting, for any $V\in{\bf C}$, a $\alpha\in\mathrm{Hom}_{\bf{C}}(V,U)$ to a $\gamma\in XV$.

The Yoneda embedding implies that the target topos contains a subcategory of spaces and the Yoneda lemma allows us to interpret the presheaves $X$ surrounding the hom-functors as spaces too. Moreover, as a topos, this new category will even be better behaved than the original one.

The co-Yoneda (for presheaves $X\in{\bf{Set}}^{\bf{C}^{op}}$) lemma and the Yoneda lemma (for functors $F\in{\bf{Set}}^{\bf{C}}$) tell us that

• $\mathrm{nat}(\mathrm{Hom}_{\bf{C}}(-,U),X)\cong XU=:{\mathrm{eval}}(X)U$

• $\mathrm{nat}(\mathrm{Hom}_{\bf{C}}(U,-),F)\cong FU=:{\mathrm{eval}}(F)U$

Meanwhile, we can form two other sets

• $\mathrm{nat}(X,\mathrm{Hom}_{\bf{C}}(-,U))=:{\mathcal O}(X)U$

• $\mathrm{nat}(F,\mathrm{Hom}_{\bf{C}}(U,-))=:\mathrm{Spec}(F)U$

and what's interesting is that those give rise two adjoint functors

${\mathcal O}:{\bf{Set}}^{\bf{C}^{op}}\longrightarrow{\bf{Set}}^{\bf{C}}$

$\mathrm{Spec}:{\bf{Set}}^{\bf{C}}\longrightarrow{\bf{Set}}^{\bf{C}^{op}}$

${\mathcal O}(X)$ corresponds to the function algebra over the would-be-space $X$. Meanwhile, $\mathrm{Spec}(F)$ is a space assigned to an algebraic structure.

nLab: Space and quantity, Yoneda lemma, Yoneda embedding

Wikipedia: Yoneda lemma

Presheaf category

Yoneda embedding