On universal morphisms
| On category theory basics $\succ$ On universal morphisms $\succ$ Foundational temp3 |
Guide
Motivation: Terminal and initial morphisms (the opposite notion, where you just flip some arrows) are called universal morphisms.
On the technical side, they are a very important concept with a ridiculously broad range of examples, because you can translate many “forall … there exists such that …” characterizations to a “there is a universal morphism such that …” characterizations. Later we'll discuss a global version, the adjunctions.
On the conceptual side, when we specify a concept using this tool we speak of “universal constructions” and the point is that they characterize things only up to isomorphism.
todo: Now it's a little difficult to fully explain the “principle of equivalence” but let me note here that the possibility to set up categories which have less arrows than the category of sets (e.g. groups and group homomorphisms are “within” sets and functions) is actually the strength of the category concept. Because then, what counts as isomorphism depends on the category and universal constructions always capture a concept up to the kind of iso in the category you consider.
| Initial object |
| Terminal object |
| Product . category theory |
| Coproduct . category theory |
| Pullback . category theory |
For clarity sake, I'm going to sketch how adjoints and their features arise from requiring universal morphisms for all objects of a category. Afterwards we take the more direct algebraic approach.
Fix a functor $G$ in ${\bf C}\longrightarrow{\bf D}$. Say now there is, for all objects $Y_i$ of ${\bf D}$, an initial morphism $\langle A_{Y_i},\eta_{Y_i}\rangle$ from $Y_i$ to $G$. Let $h_{12}:\mathrm{Hom}(Y_1,Y_2)$ and let $h_{12}':=\eta_2\circ h_{12}$. By the initial property, there is a morphism $g_{12}:\mathrm{Hom}(A_{Y_1},A_{Y_2})$ for $h_{12}'$.
(quite different notation)
We'll now set up a functor $F$ in ${\bf D}\longrightarrow{\bf C}$ with object map $FY_i=A_{Y_i}$ and arrow map $\mathrm{Hom}(Y_i,Y_j)\to\mathrm{Hom}(A_{Y_i},A_{Y_j})$ according to, e.g. $F(h_{ij}):=g_{ij}$. This is an so called adjoint functor to $G$. Note that the above diagram now also tells us that the $\eta_{Y_i}$ are the components of a natural transformation $\eta:\mathrm{nat}(1_{\bf D},GF)$.
Consider now a $X$ in ${\bf C}$. By our initial assumption, we know that in ${\bf D}$, there is an initial morphism $\langle FGX,\eta_{GX}\rangle$. Using the initial property for $h'=1_{GX}$ now provides us with an arrow $\epsilon_X:\mathrm{Hom}_{\bf C}(FGX,X)$. Moreover, drawing the diagrams immediately tells us that $G(\varepsilon_X)\circ \eta_{GX}=1_{GX}$ and, after applying $F$ to that digramm, $\varepsilon_{FY}\circ F(\eta_Y)=1_{FY}$.
(…) after more (tedious) work, we could show that $\epsilon_X$ also make up the components of a natural transformation $\epsilon:\mathrm{nat}(FG,1_{\bf C})$. And then it also follows that $\epsilon_X$ is always a terminal morphism from $F$ to $X$.
Instead of stating out with a functor so that each object defines a universal morphism, the counit-unit approach to adjunctions starts out with two natural transformations $\langle\varepsilon,\eta\rangle$, which satisfy the two algebraic relations described above.
(…) Again, after some work, the universality properties can then be shown, so the approaches are equivalent.
Here an image displaying the terminal/initial roles of the the natural transformations:
The picture above makes it clear how $f\mapsto G(f)\circ\eta_Y=g$ and $g\mapsto \epsilon_X\circ F(g)=f$ put ${\bf C}[FY,X]$ and ${\bf D}[Y,GX]$ in bijection. In ${\bf{Set}}$ the bijection described above is a natural isomorphism between the functors $\mathrm{Hom}_{\bf C}(F-,=)$ and $\mathrm{Hom}_{\bf D}(-,G=)$. The following captures those maps
Idea
What functors do is mapping objects $A$ and $B$ from a category to objects $FA$ and $FB$ in another category. Important for the following is that when doing this, they don't “look inside” the object that they map, or manipulate their content. E.g. in the category of sets, a functor $F$ might map $\mathbb N$ to $F\mathbb N$, but here nothing is said about individual numbers being mapped. On the other hand, there can be several arrows between two objects and a functor transforms each of them individually. E.g. if $f,g,h:{\bf D}[A,B]$, then $F(f),F(g),F(h):{\bf C}[FA,FB]$. And a functor $F$, per definition, always preserves the arrow structure (commutative triagles). There is more going on with arrows than with objects. A natural transformation, redirecting one functor $F$ to another functor $F'$, is different however. Because a for every object $A$, a natural transformation is an arrow between $FA$ and $F'A$. E.g. if $F$ and $F'$ map to sets (or types), the natural transformation is actually a function on their elements (or terms).
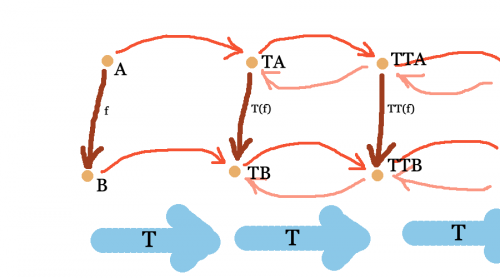
One could now say a monad is the best of both worlds: It concerns
- an endo-functor $T$ which shifts the arrow structure within a category
- two families of natural arrows between objects in the category, which flow with and against the shifts and, naturally, respects all of the structure. Let's take $TX$ to be the object of interest, generated via $T$ and with reference to $X$. Then $\eta$ and $\mu$ identify, although in two different ways: $\eta$ embeds $X$, and $\mu$ corrects from what's in $TTX$.
And here is a consequence of the monad definition: Let $i,j,n,m\ge 0$. For any $f:T^iA\to B$, you can get a $f':T^nA\to T^mB$. For any $g:T^iA\to T^{j+1}B$, you can get a $g:A^n\to T^{m+1}B$.
How do monads arise from adjunctions
TODO: Redo the mental image here (according to e.g. MacLane and the pic on Wikipedi, right to left, etc.)
todo: make new pictures where the names ${\bf C}$ and ${\bf D}$ are reversed…because that's the usual notation.
Every hom-class adjunction gives rise to a monad (we show this now) and it actually turns out that all monads arise this way. We are going to show how.
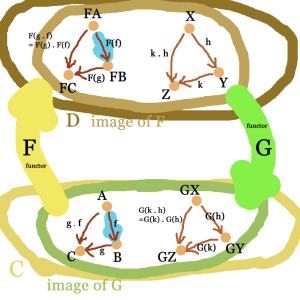
For startest, we are given two functors $F$ and $G$ which map between categories ${\bf C},{\bf D}$, but in opposite directions. Here a picture of the situation:
The above definition says that a hom-class adjunction $\Phi$ provides us, for any two objects $P\in{\bf C}$ and $Q\in{\bf D}$, with a natural bijection between the arrows in ${\bf D}[FP,Q]$ and ${\bf C}[P,GQ]$. This means that a huge part of the arrow structure in one category can be rediscovered in the other!
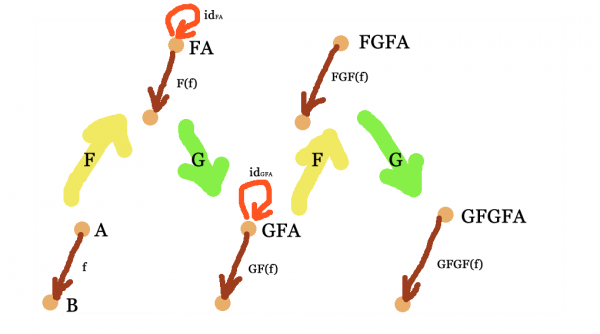
Say we have two functors $F,G$ as above. Pic any object $A\in\mathrm{Ob}_{\bf C}$ and consecutively apply the functors $F,G$ to it. You can imagine this as a zigzag-movment.
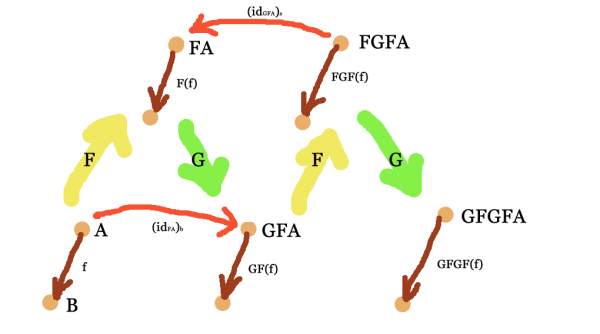
Now say we have a hom-class adjunction between the two functors, i.e. a natural isomorphism between ${\bf C}[-,G=]$ and ${\bf D}[F-,=]$. Consider the hom-class ${\bf D}[FA,FA]$ at the single object $FA$. It is in bijection with ${\bf C}[A,GFA]$, i.e. for every $f:{\bf D}[FA,FA]$ in ${\bf D}$, there is a $\Phi(f):{\bf C}[A,GFA]$ in ${\bf C}$. We know at least one arrow in $f:{\bf D}[FA,FA]$, namely the identity. Because the functors $F,G$ as well as the natural transformation $\Phi(f)$ at the object respects structure, we just obtained a natural transformation $\Phi(1_{FA})$ at the object within ${\bf C}$. (Sometimes, the downwards/upwards transformations $\Phi/\Phi^{-1}$ are sometimes denoted flat/sharp.)
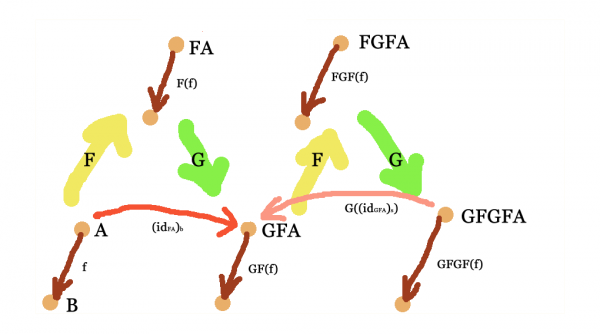
Similarly, we can consider $\Phi^{-1}(1_{GFA})$, which is a natural transformation in ${\bf D}$. We can map this back to ${\bf C}$ via $G$ and obtain a natural transformation $G\left(\Phi^{-1}(1_{GFA})\right)$ which runs in the opposite direction. (Remark: Conversely, the hom-class adjunction is given by first applying the functor and then the suitable natural transformation.)
In the remainder of this entry, we’re going to write $T:=GF$.
That’s it, we can now shift the complete structure of ${\bf C}$ within ${\bf C}$!
(Remark: Changing up the definitions so that everything lives in the other category gives a comonad.)