Extended quantum action functional . finite
Partial function
| context | $ \mathbb K = \mathbb C \lor \mathbb R $ |
| context | $ m\in\mathbb N $ |
| context | $ D $ …. self-adjoint operator in $\mathbb K^m$ with well behaved inverse at least for $D+i\,\varepsilon\,\mathrm 1$ |
| definiendum | $Z:(\mathbb K^2\to\mathbb R)\to \mathbb K^4\to \mathbb K $ |
| definiendum | $Z_{\mathcal L_\mathrm{int}}(J,K,\phi,\psi):=\mathrm{e}^{i\hbar^{-1}\sum_{i=1}^m\mathcal L_\mathrm{int}\left(-i\,\hbar\frac{\partial}{\partial J_i},-i\,\hbar\frac{\partial}{\partial K_i}\right)} \left( \mathrm{e}^{i\,\hbar^{-1} \left\langle J\left|\,\mathcal{R}_\varepsilon\,\right|K\right\rangle}\cdot\mathrm{e}^{Z_\text{source}(J,K,\phi,\psi)}\right)$ |
| $\mathcal{R}_\varepsilon\equiv-\left(D+i\,\varepsilon\,\mathrm{1}\right)^{-1}$ |
| $Z_\text{source}(J,K,\phi,\psi):=i\,\hbar^{-1}\left(\left\langle J\left|\right. \phi\right\rangle+\left\langle K\left|\right. \psi\right\rangle\right)$ |
Discussion
The operator $\mathcal{R}_\varepsilon$ is denoted the response function because it relates the classical free field to the source, $(D+i\,\varepsilon)\phi=-J$. The brackets are the standard inner product on $\mathbb C^n$ or $\mathbb R^n$. The finite quantum action functional presented here can be generalized by
- considering an infinite set (spacetime manifold) instead of $\{1,2,\dots,m\}$, in which case the sums $\langle a|b \rangle$ become integrals
- consider non-scalar fields, which introduces even more indices and the possibility for much more complicated operators $D$.
The factor involving $Z_\text{source}$ is the only one involving arguments $\phi$ and $\psi$ and it's essentially only there to formulate some identies (LSZ reduction formula). In the discussion below we only consider the case $\phi=\psi=0$.
The expression
$Z_{\mathcal L_\mathrm{int}}(J,K,0,0)=\mathrm{e}^{i\hbar^{-1}\sum_{i=1}^m\mathcal L_\mathrm{int}\left(-i\hbar\frac{\partial}{\partial J_i},-i\hbar\frac{\partial}{\partial K_i}\right)}\mathrm{e}^{i\hbar^{-1} \left\langle J\left|\,\mathcal{R}_\varepsilon\,\right|K\right\rangle}$
should be interpreted as the solution of an integral as presented in magic Gaussian integral. Reminder: In one dimension it reads
$\int_{-\infty}^\infty\,f(\phi)\,\mathrm{e}^{-\tfrac{1}{2}a\,\phi^2+i\,\phi\,j}\mathrm d\phi \ \propto \ f\left(-i\frac{\partial}{\partial j}\right)\,\mathrm e^{-\tfrac{1}{2}j^2\,a^{-1}}$
Indeed, for $\mathbb K:=\mathbb R$ it equals a finite dimensional (path) integral
$Z_{\mathcal L_\mathrm{int}}(J,K,0,0) = \mathcal N\cdot\lim_{\varepsilon,\eta\to 0}\int_{-\infty}^\infty \mathrm e^{i\,\hbar^{-1}\,S(J,K,\phi,\psi)}\prod_{i=1}^m \mathrm d\phi_i\,\mathrm d\psi_i$
Here $\mathcal N$ is a normalization constant and $S(J,K,\phi,\psi)$ is the sum of the following terms
$S_\text{free}:=\left\langle\psi\left|\,D\,\right|\phi\right\rangle$
$S_\text{int}:=\sum_{i=1}^m {\mathcal L_\mathrm{int}}(\phi_i,\psi_i) $
$S_\text{source}:=\left\langle J\left|\right. \phi\right\rangle+\left\langle K\left|\right. \psi\right\rangle$
$\mathfrak{reg}:=-\varepsilon\,\left\langle\phi\left|\right.\phi\right\rangle-\eta\,\left\langle\psi\left|\right.\psi\right\rangle$
To elaborate on that consider now, for simplicity, the “only one kind of particle”-case
$\mathcal N\cdot\lim_{\varepsilon\to 0}\int_{-\infty}^\infty \mathrm e^{i\,\hbar^{-1}\,S(J,\phi)}\prod_{i=1}^m \mathrm d\phi_i$
with one source $J$ and field $\phi$. Consider
$"\mathcal N'\cdot\int_{-\infty}^\infty\,(1+(i\,\hbar^{-1})\,\phi\,J+(i\,\hbar^{-1})^2\,\phi^2\,J^2+\dots)\,\mathrm{e}^{i\,\hbar^{-1}\,\left(S_\text{free}(\phi)+S_\text{int}(\phi)\right)}\mathcal D\phi"$
which is analog to the probability theoretic characteristic function $\mathrm{{\bf E}}[\mathrm{e}^{i\,\hbar^{-1}\left\langle J\left|\right. \phi\right\rangle}]$. The point is that this generating functional of the path integrals equals the quantum action functional which, by the interpretation given in retarded propagator, encodes the correlation functions/transition amplitudes $C_k(i_1,i_2,\dots,i_m)$ of the theory:
$ Z(J) = \sum_{j=0}^\infty \frac{i^j}{j!\hbar^j}\sum_{i_0,\dots,i_j=1}^m C_j(i_1,\dots,i_j)\prod_{l=0}^jJ_j = $
$ =C_0^\phi+\frac{i}{\hbar}\sum_{k=1}^m C_2(k)\,J_k+\frac{i^2}{2!\hbar^2}\sum_{k,j=1}^m C_1(k,j)\,J_k\,J_j+\dots $
Example
Consider the so called $\phi^4$-theory given via $D=\Box+m^2$ and $\mathcal L_\text{int}(\phi)=-\lambda\,\phi^4$. Then the quantum action functional reads
$\mathrm{e}^{i\,\hbar^{-1}\cdot\lambda\sum_{j=1}^m\left(-i\,\hbar\frac{\partial}{\partial J_j}\right)^4} \mathrm{e}^{i\,\hbar^{-1} \left\langle J\left|\,-\left(\Box+m^2+i\,\varepsilon\,\mathrm{1}\right)^{-1}\,\right|J\right\rangle}$
One is interested in the functions $C$ which encode all observables of the theory. For a given process of interest (e.g. scattering of particles from and to some spacetime points which are given by certain $j$-values) one must expand $Z$ in $J$'s and powers of the coupling, $\lambda^k$, and read off the $C$-coefficient. However, the expression is very labourious to compute. Note that the $J$-derivatives produce complicated sums, e.g.
$\sum_j \frac{\partial}{\partial J_j}\sum_i \sum_l\,f(J_i,J_l)=\sum_j \sum_i \left(f^{(1,0)}(J_j,J_i)+f^{(0,1)}(J_i,J_j)\right)$,
and so a summand
$\lambda^k\sum_{j=1}^m\left(-i\,\hbar\frac{\partial}{\partial J_j}\right)^{2k}\,\left\langle J\left|\,-\left(\Box+m^2+i\,\varepsilon\,\mathrm{1}\right)^{-1}\,\right|J\right\rangle^n$
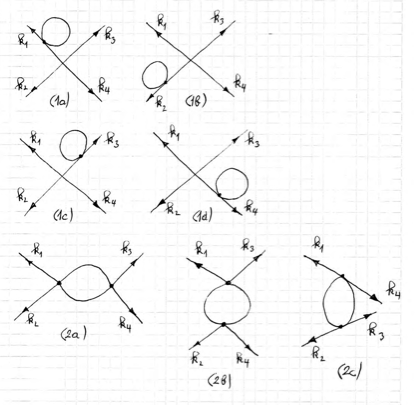
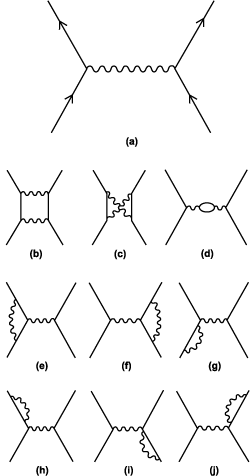
is extremely messy. The nice thing, though, is that each term in the expansion can be represented by a Feynman diagram. The external lines translate to the choosen spacetime points $j$, the internal lines to the inverse operator of the theory (propagator) and the internal vertices to the coupling constants $\lambda$ plus sums like above. Below are the $\lambda^0,\lambda^1$ and $\lambda^2$ terms for the process with four points (expressed in momentum space).
In the discrete case, the “Differential operators” are just value differences of the field on neighboring points. The operator is a matrix e.g. with some entries above the diagonal. The action involves sums over term involving that matrix. In the continuum limit the derivatives of the inner products $\langle J|(\dots)^{-1}|J\rangle$ become very tricky integrals. By passing to momentum space, the different or differential operators can be multiplicatively invertex, because e.g $\Box$ just becomes $k^2$. The Feynman rules of a theory are the ad hoc rules of how to compute the correlation functions from the diagrams
The order of the internal vertices is four because the expression $\left(-i\hbar\frac{\partial}{\partial J_i}\right)^4$ always brings down four $\phi$'s at a time.
Conversely, in the quantum electrodynamics Lagrangian
$\mathcal{L}^\text{QED} = - \tfrac{1}{4} (\partial_\mu A_\nu - \partial_\nu A_\mu)(\partial^\mu A^\nu - \partial^\nu A^\mu) + \sum_n^\text{#fermions} \bar\psi_n (i \gamma^\mu (\partial_\mu+ieA_\mu) -m_n) \psi_n$
the interaction term
$\mathcal{L}_\text{int}^\text{QED}=-e\,\left({\bar\psi}\,\gamma^\mu\,\psi\right)\,A_\mu$
always brings together two fermion lines and one wiggly photon line